医学論文を投稿すると、医学的なレビューの他に、統計レビュアーから統計学的なコメントを受けることがあります。統計レビュアーのコメントは専門的なことが多く、
「何を言っているのか分からない…」と頭を抱えたことはないでしょうか?
今回はその統計レビュアーが論文によく付けた14のコメントを解説した論文”Statistical review: frequently given comments”を現役統計家の観点から解説します!
「どういったコメントが付きやすいか」を理解することで、統計レビュアーへの対策になりますので、是非参考にしてみてください!
超大作となってしまったので目次から興味のあるセクションからご覧ください!
統計家がよく付ける14のコメント

今回はAnnals of the Rheumatic Diseases (ARD)に投稿された”Statistical review: frequently given comments”という論文について解説します。
この論文の筆者である生物統計家のStian Lydersen先生はノルウェー科学技術大学の教授であり、2006年-2014年までに約200報の論文の統計レビューを行ったそうです。
この論文ではStian Lydersen先生がレビューを行う中でよく指摘していた14のコメントについてまとめられています。
Stian Lydersen先生がよく指摘していた14のコメントは以下になります(日本語訳はRio作)。
統計家がよく付ける14のコメント
- 解析方法に対するコメント
- Report how missing data were handled.
欠測データの取り扱い - Limit the number of covariates in regression analyses.
回帰モデルを使った解析の説明変数の個数 - Do not use stepwise selection of covariates.
変数選択にステップワイズ法を用いないこと - Use analysis of covariance (ANCOVA) to adjust for baseline values in randomised controlled trials.
ランダム化比較試験ではベースライン値の調整にANCOVAを用いること - Do not use ANCOVA to adjust for baseline values in observational studies.
観察研究ではベースライン値の調整にANCOVAを用いないこと - Dichotomising a continuous variable: a bad idea.
連続値を二分することはいいアイデアではない - Student’s t test is better than non-parametric tests.
ノンパラメトリック検定よりt検定の方が優れている - Do not use Yates’ continuity correction.
イェーツの補正を用いないこと - Mean (SD) is also relevant for non-normally distributed data.
平均とSDは正規分布ではないデータにも関係する - Report estimate, CI and (possibly) p value—in that order of importance.
推定値、信頼区間、p値の順に重要である
- Report how missing data were handled.
- 不要な解析に対するコメント
- Post hoc power calculations—do not do it.
事後的な検出力の計算は行ってはいけない - Do not test for baseline imbalances in a randomised controlled trial.
ランダム化比較試験では患者背景を検定で比較しないこと
- Post hoc power calculations—do not do it.
- 報告方法に対するコメント
- Report actual p values with 2 digits, maximum 3 decimals.
実際のp値を2桁、最大小数点以下3桁で報告すること - Format for reporting CIs.
信頼区間の報告フォーマットを確認すること
- Report actual p values with 2 digits, maximum 3 decimals.
1-10は解析方法に対するコメント、11-12は不要な解析に対するコメント、13-14は報告方法に対するコメントになります。
以降ではそれぞれのコメントを解説して、部分的には私見で補足していきます!
解析方法に対するコメント

Report how missing data were handled.(欠測データの取り扱い)
欠測値を取り扱う際にはよく欠測値を補完する方法や欠測のない症例に絞った完全データ解析が行われます。筆者は補完法の中でも特に最後に確認された測定値で欠測値を補完するLOCF(last-observation-carried-forward)は使うべきではありません。
補足:複数の欠測値の扱い方法で解析する感度解析が重要!
欠測値の取り扱いはどのようなメカニズムで欠測が発生したかによって、その取り扱いを考える必要があります。ただ多くの場合、この欠測メカニズムは特定できません。
そのため、複数の方法で欠測を取り扱った解析(感度解析)を行うことで、欠測の影響を考察することをお勧めします!
詳細は以下に記載しているので是非参考にしてみてください!
Limit the number of covariates in regression analyses.(回帰モデルを使った解析の説明変数の個数)
回帰モデルに含める説明変数の数が症例数に対して多い研究が多くあります。説明変数の数は症例数:説明変数=10:1の比を目安に決めるべきとされています。ただし、この症例数と説明変数の比は目安であり、症例数:説明変数=15:1、20:1など複数の基準が主張されています。ただ筆者(Stian Lydersen先生)の経験としては症例数:説明変数=5:1で十分と考えます。
この症例数と説明変数の比を考えるときに注意が必要なのは、説明変数の数は症例数よりもデータの情報量に依存します。データの情報量の計算方法は解析の方法によって異なり、ロジスティック回帰モデルでは結果変数のありなしのうち少ない方の症例数、Cox回帰モデルであればイベント数が情報量になります。
補足:どうして情報量と症例数の比は考える必要がある?
説明変数の数に対して十分なデータの情報量が必要なのは、層(説明変数の組み合わせ)内の症例数が少なくなり、層内の効果の推定が安定しないからです。また説明変数が少なくても説明変数間で相関があると層間で症例数が偏ってしまい、効果の推定が不安定になってしまいます。
そのため、説明変数の数とデータの情報量の比が十分でも推定が不安定になることがあるので、あくまで5:1や10:1はあくまで目安として、信頼区間などで効果の推定が安定しているか確認する必要があります。
Do not use stepwise selection of covariates.(変数選択にステップワイズ法を用いないこと)
説明変数を選択する際に機械的に変数を選択する方法が頻用されてきました。ただし、近年機械的な変数選択には批判的な声が上がっています。その理由として、このような変数選択は統計学的、論理的な正当性が欠けていること、推定にバイアスが入ってしまうことが挙げられます。
そのため、説明変数はclinical questionと臨床的な観点から選択されるべきです。
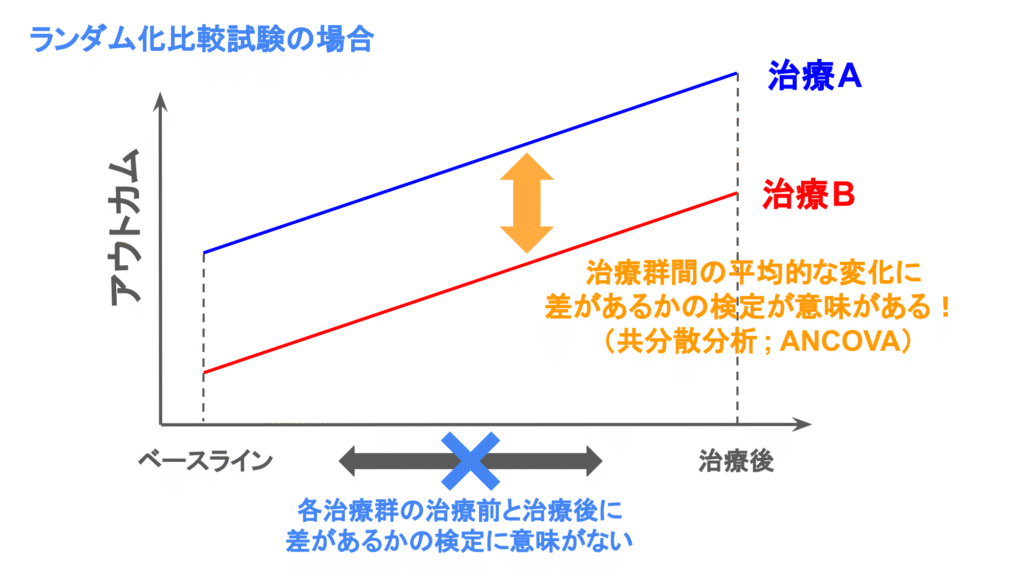
Use analysis of covariance (ANCOVA) to adjust for baseline values in randomised controlled trials.(ランダム化比較試験ではベースライン値の調整にANCOVAを用いること)
2つの治療群において、アウトカムがそれぞれ治療前と治療後に測定されるランダム化比較試験を想定します。各治療群ごとに治療前と治療後のアウトカムを比較することは妥当ではありません。治療群間でアウトカムを比較したいときには、治療群間の平均変化を比較することには意味があります。この良い解析方法は治療後の結果を結果変数、ベースライン値と治療群を説明変数として回帰モデル(共分散分析; ANCOVA)によって、治療群間の平均変化を比較する方法です。
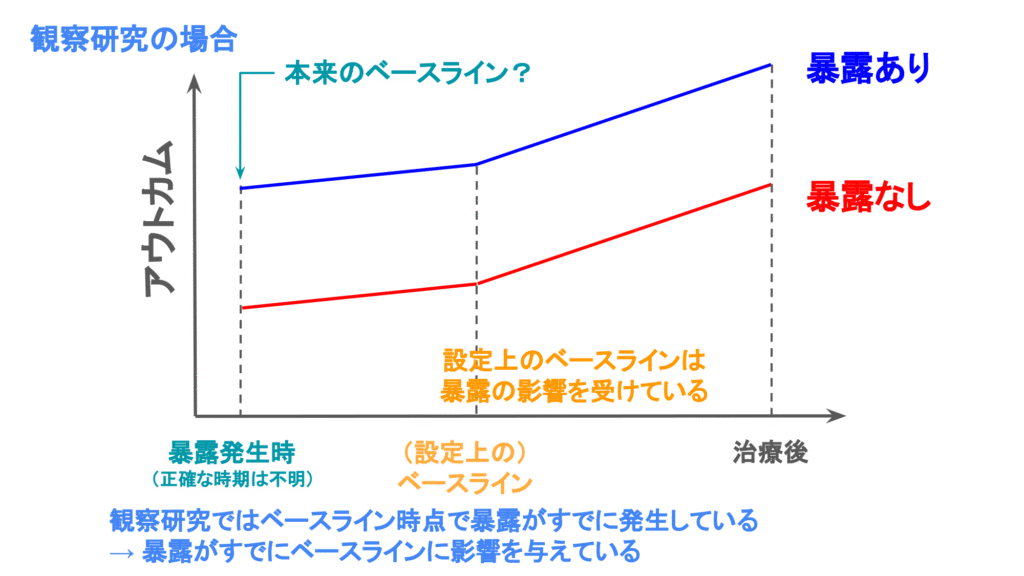
Do not use ANCOVA to adjust for baseline values in observational studies.(観察研究ではベースライン値の調整にANCOVAを用いないこと)
ランダム化比較試験で推奨された共分散分析は観察研究では推奨されません。ランダム化比較試験では、ベースライン測定後に治療が行われます。一方で、観察研究ではベースラインと設定時点ですでに暴露が起こっている可能性があり、ベースライン値が暴露の影響を受けている可能性があります。そのため、観察研究で共分散分析を用いるとバイアスが生じえます。
Dichotomising a continuous variable: a bad idea.(連続値を二分することはいいアイデアではない)
連続値データを二値に分けることは情報量の損失につながるため避けるべきです。また二値に分けるということは閾値によって、アウトカムがその閾値によって階段的に変化するという仮定をおいています(補足:例えば、年齢を65歳未満、65歳以上で分けた場合は、65歳を境にリスクが何倍になる、という仮定を置いていることになります)。
特に中央値を閾値として分類していることがよく見られますが、中央値による二値化は好ましくありません。もし二値に分類したいときには臨床的な閾値を使うべきです。
補足:連続値として扱うことにもリスクがある!
連続値をやみくもに二値に分けることは避けるべき、という意見には賛同します。ただ連続値のまま扱うことにも統計学的に強い仮定を置くことになるため注意が必要です。
例えば、回帰モデルにおいてある疾患のリスクを年齢で説明できるか、を調べたいとします。このとき、年齢を連続値で扱うと、「1歳ごとにリスクが何倍になる」という仮定を置いていることになります。つまり、20歳→30歳へ上がるときに上がる疾患リスクと50歳→60歳へ上がるときに上がる疾患リスクは同じである、という解釈になります。
そのため、連続値のまま扱うことにも統計学的に妥当ではない仮定を置いてしまうというリスクがあります。
どうしても連続的に扱うことが妥当ではなく、臨床的に閾値が決められない場合には、二値ではなく、三値以上に分けて検討することも一案です。もし三値以上に分けて、アウトカムの単調性が確認できれば、連続値として扱うことが妥当とすることができます。
Student’s t test is better than non-parametric tests.(ノンパラメトリック検定よりt検定の方が優れている)
平均値を比較する検定手法としてt分布を前提としたパラメトリック検定法であるStudentの t 検定や分布を仮定しないノンパラメトリック検定法であるWilcoxon 検定が使われます。一般にStudentの t 検定はWilcoxon 検定よりも利点があります。大きく3つあり、
- p値だけでなく平均値の信頼区間を計算できること
- 症例数が小さいときにもStudentの t 検定は強力な検定方法であること
- 他の検定手法と関連があり一貫性が保たれること
です。
またStudentの t 検定は正規性が成り立たない場合にも頑健な方法であることが分かっています。この正規性はP-Pプロットではなく、Q-Qプロットを使って確認することができます。もし正規性から外れているときにもブートストラップを使って信頼区間やp値を計算することができます。
補足:Studentの t 検定は外れ値の影響を受けるので注意!
Studentの t 検定のようなパラメトリック検定は分布を前提とした検定方法です。そのため、一般にデータが前提とする分布に従わない場合にはノンパラメトリック検定を使われます。著者はStudentの t 検定の方がそのような状況でもStudentの t 検定はWilcoxon 検定より利点があるというように説明されています。
ただ状況によってはWilcoxon 検定が妥当であることがあります。それはデータに外れ値が含まれる場合。Studentの t 検定は外れ値の影響を強く受けてしまうので、外れ値が含まれるときには外れ値に頑健なノンパラメトリック検定を使う方がよいでしょう!
Do not use Yates’ continuity correction.(イェーツの補正を用いないこと)
2つの割合を比較するときにはカイ二乗検定や正確検定が使われます。伝統的に推奨される検定法はセルの症例数によって変わります。基準となるのは「セルの症例数が5以上かどうか」ということです。もしセルの症例数が5以上であればカイ二乗検定、5未満であれば正確検定が推奨されます。
場合によってはカイ二乗検定を行うときにイェーツの補正が用いられることがあります。このイェーツの補正は計算負荷の問題からやむを得ず用いられていた方法です。そのため、コンピュータが発展した今、使うべきではありません。
補足:現代でも正確検定は時間がかかる!
イェーツの補正は離散型のデータを連続値の分布であるカイ二乗分布に近似するときに保守的になる(有意になりにくい)ように補正をかける方法です。
イェーツの補正が用いられた経緯としてコンピュータが今ほど発展していなかった、ということがあります。正確検定は取りうる全ての結果の確率を計算する必要があるため、手計算での計算は困難です。そのため、イェーツの補正はコンピュータが発展していない時代には計算時間を節約できて重宝されていました。
ただ現代でも正確検定は症例数が多すぎる場合には、計算時間がかかることがあります。そのため、時間がかかるから計算が間違っている!と誤解しないようにしましょう(200-300例の正確検定で30分ぐらいかかったことがあります…)。
Mean (SD) is also relevant for non-normally distributed data.(平均とSDは正規分布ではないデータにも関係する)
平均と標準偏差はデータが正規分布に従っていない場合にも意味のある指標です。多くの統計家がデータが正規分布に従っていない場合には中央値や四分位範囲を使うべきと主張しています。ただこれは誤解であり、メタ解析に有用であるなど平均と標準偏差には大きなメリットがあります。
補足:中央値や四分位範囲も重要!
この意見を解釈する上で注意が必要なのは「平均値と標準偏差のみ報告すればよい」ということではない、ということです。つまり、データが正規分布に従わない場合でも、中央値や四分位範囲に加えて、平均値と標準偏差も報告すべき、というように解釈する必要があります。
ただこの意見には同意できない部分もあります。というのも、データが正規分布に従わない場合には、データの分布に対して読者の誤解を招く可能性があります。
有名な平均値と標準偏差の関係として、「平均値±2×標準偏差の中にはデータの95%が含まれる」というものがあります。これは正規分布に従っているときにのみ成り立つ関係です。そのため、もしデータが正規分布に従っていないときは平均値と標準偏差に加えて、中央値や四分位範囲も報告すべきです。
Report estimate, CI and (possibly) p value—in that order of importance.(推定値、信頼区間、p値の順に重要である)
p値は医学研究にとどまらず、多くの応用科学論文において誤用されています。この問題はNature誌の投稿ガイドラインでも述べられており、p値だけではなく推定値や信頼区間も示す必要があります。
補足:p値は誤用されるので注意!
よくp値が誤用されていることに強く同意します!
この詳細は以下にまとめていますので、是非参考にしてみてください!
またp値の誤用は国際的な統計学会からASA声明としてまとめられていますので、ご参考まで!
不要な解析に関するコメント

Post hoc power calculations—do not do it.(事後的な検出力の計算は行ってはいけない)
一部のジャーナルでは推奨されているが、事後的な検出力計算は無駄である。検出力はまだ行われていない研究で帰無仮説が棄却される確率であり、すでに実施された研究で帰無仮説が棄却されると検出力は0となる。そのため、研究後の検出力は統計学的に解釈ができない。
補足:検出力とp値は対応した指標であるため注意が必要!
これは専門的すぎる解説なので「事後的な検出力計算は不要である」と理解することで十分かと思います。
そもそも何故事後的な検出力計算が求められるのでしょうか?その理由として「統計学的に有意差が示されなかった理由を特定するため」ということが考えられます。
一般に検出力は症例数が増加するほど高くなることが知られています。そのため、統計学的有意差が示されなかった原因が「臨床的に意味のある差が得られなかったから」なのか、「症例数が不足していて検出力が十分ではなかったから」なのか、考察を深めるために事後的な検出力計算が求められているのだと考えられます。
ただ多くの場合、事後的な検出力が求められるのは、観察研究のような後ろ向き研究において有意差が示されなかった場合です。そもそもこのような研究では検定やそのp値で評価することは妥当ではありません。そのため、p値と関連する事後的な検出力ではなく、オッズ比やハザード比といった推定値やその信頼区間で、効果を評価する必要があります。
Do not test for baseline imbalances in a randomised controlled trial.(ランダム化比較試験では患者背景を検定で比較しないこと)
ランダム化比較試験の結果を報告するときには、治療群ごとにベースライン時点の患者背景を表として示すことが推奨されます。多くの医学雑誌ではベースライン時点の不均衡を比較するために検定によるp値が示されています。ただ、このp値は不要な指標です。CONSORTガイドラインでも推奨されていません。またランダム化が適切に行われているとすると、有意水準5%の設定下では、5%の患者背景に有意差が見られると予想できます。
補足:ベースライン値を検定すると検定の多重性が問題に!
RCTのみならず、観察研究でも検定によるベースラインの比較は不要です!
というのも、検定を繰り返すことで検定の多重性が問題となります。つまり、検定を繰り返せば、差がなくても有意差あり、と判定される確率が上がるということです。
また、有意水準というのは「差がないときに誤って差があると言っていいのは何%か」を示した基準です。もし有意水準が5%であれば、差がない状況で100回の検定を行えば、5回は誤って差があると判定してよい、ということになります。
そのため、患者背景をやみくもに検定して比較することは、偶然の差を特定している作業に他ならないため不要です。
報告方法に対するコメント

以下2つは報告方法に関するコメントです。
- Report actual p values with 2 digits, maximum 3 decimals.(実際のp値を2桁、最大小数点以下3桁で報告すること)
- Format for reporting CIs.(信頼区間の報告フォーマットを確認すること)
ただ報告フォーマットは投稿するJournalのガイドラインによって変わってきます。そのため、報告フォーマットはJournalの投稿規定を確認して、Journalにあわせた報告を行いましょう!
まとめ
今回はAnnals of the Rheumatic Diseases (ARD)に投稿された”Statistical review: frequently given comments”から「統計家がよく付ける14のコメント」を解説しました!
統計レビュアーからのコメントは専門的なコメントがつくことがあります。ただ「どのようなコメントがつくのか」を知っておくと、事前に準備することができます!
この記事を参考にして、論文のアクセプトに貢献できたならうれしいです!











コメント