【マッチング比はどれぐらいがいいの？】傾向スコアマッチングの最適なマッチング比とマッチング比の考え方を解説！

疫学研究、とりわけ後ろ向きの研究では傾向スコアを使った解析がよく行われます。

傾向スコアを使った解析で最もよく用いられるのが傾向スコアマッチングです。
傾向スコアマッチングは傾向スコアが似た症例を群間でマッチングして解析対象を選択する方法で、マッチング後は平均的に患者背景がそろうことが分かっています。

傾向スコアマッチングの中でも問題になるのが「群間のマッチング比率をどの程度にするか」ということ。

今回は傾向スコアマッチングのマッチング比率を検証した論文を参考に、
傾向スコアマッチングの最適なマッチング比率とマッチング比率の考え方について解説します！

傾向スコアと傾向スコアマッチングとは？

最適なマッチング比に入る前に傾向スコアと傾向スコアマッチングについて復習しておきましょう！

傾向スコアとは？

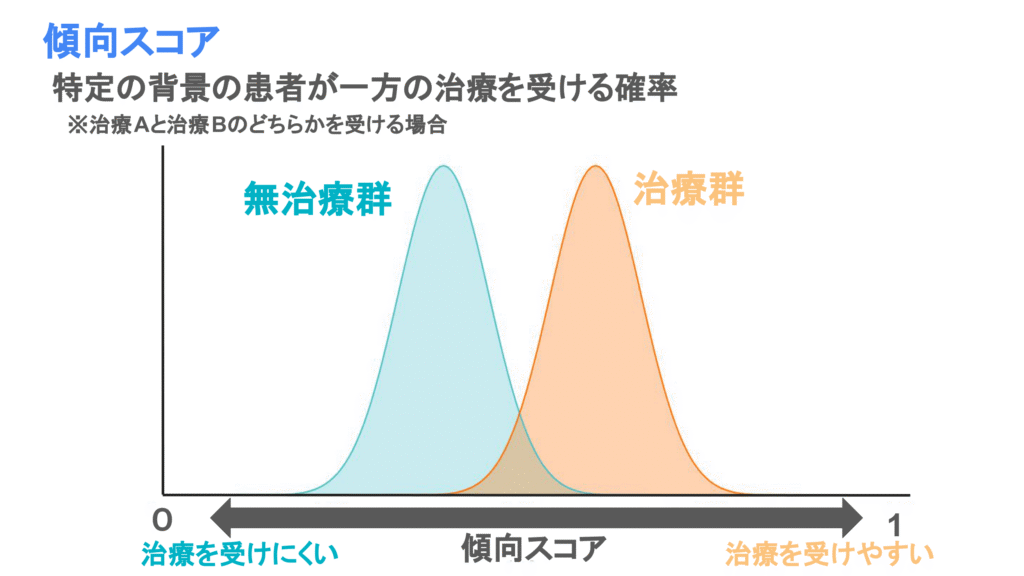
傾向スコアとは「ある患者背景を有する症例が治療を受ける確率」のことです。

傾向スコアは0~1の値に収まり、0〜0.5のときは治療を受けにい患者、0.5〜1のときは治療を受けやすい患者と判断することができます。

傾向スコアについてさらに詳しく知りたい方は以下をご覧ください。

傾向スコアマッチングとは？

傾向スコアを使った解析には様々ありますが、その中でも代表的な解析方法が傾向スコアマッチングです。

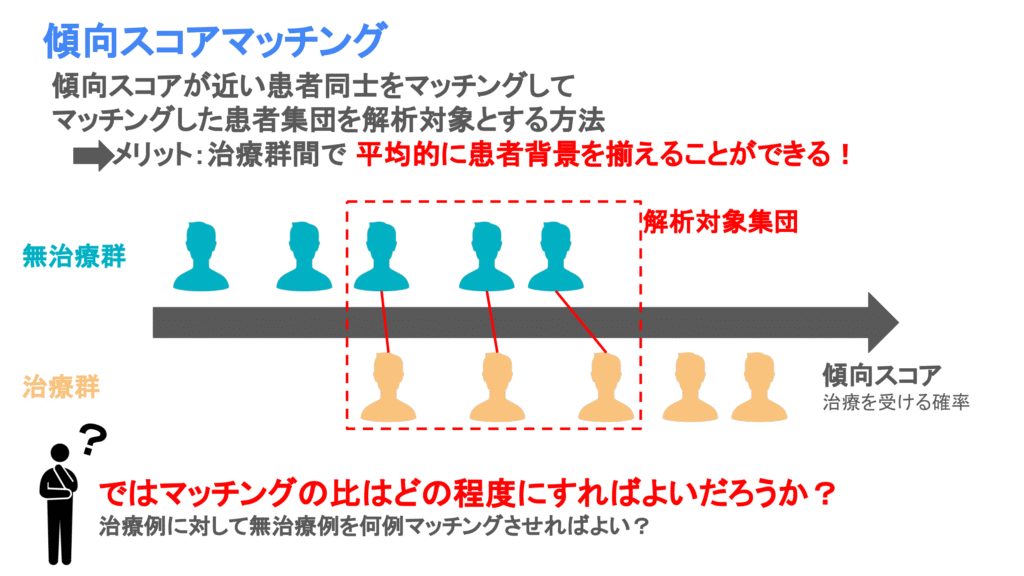
傾向スコアマッチングは傾向スコアが似通った人をマッチングして解析対象を決める方法です。傾向スコアが似ているということは、傾向スコアの算出に至った患者背景が似ていると考えられます。そのため、傾向スコアを似ている人同士をマッチングさせることで、治療群間で平均的に患者背景を揃えることが可能になります。

傾向スコアマッチングの方法は様々あり、それぞれで設定するパラメータが異なります。ただどのマッチング手法においても問題になるのは、マッチング比率です。つまり、治療群の例数に対して無治療群の例数を何倍とってくるか、が問題となります。

この記事ではその最適なマッチング比率とマッチング比率の考え方について解説します！

マッチング比率の考え方と最適なマッチング比率

取り扱う論文と最適なマッチング比率

傾向スコアマッチングのマッチング比に関する研究は様々ありますが、この記事では以下の研究を参考にします。この論文はコンピュータ上で様々な状況を想定して、そのもとで最適なマッチング比を議論した論文です。論文の結論では、最適なマッチング比率は1:1または1:2であると言われています。

マッチング比率による解析結果への影響

ではなぜマッチング比率を考える必要があるのか、その上でなぜ最適なマッチング比率が1:1または1:2とされているのでしょうか？

実はマッチング比率は解析結果に以下のような影響を及ぼします。

マッチング比率	メリット	デメリット
小さい場合（1:1, 1:2）	患者背景が揃いやすいバイアスが小さくなる	マッチングされなかった患者のデータを捨てることになる
大きい場合（1:10, 1:100)	推定値のバラつきが小さくなる解析対象例が増える	バイアスが大きくなる

以下では、マッチング比率によって解析結果にどのような影響があるのかを説明していきます。

マッチング比率が小さい場合

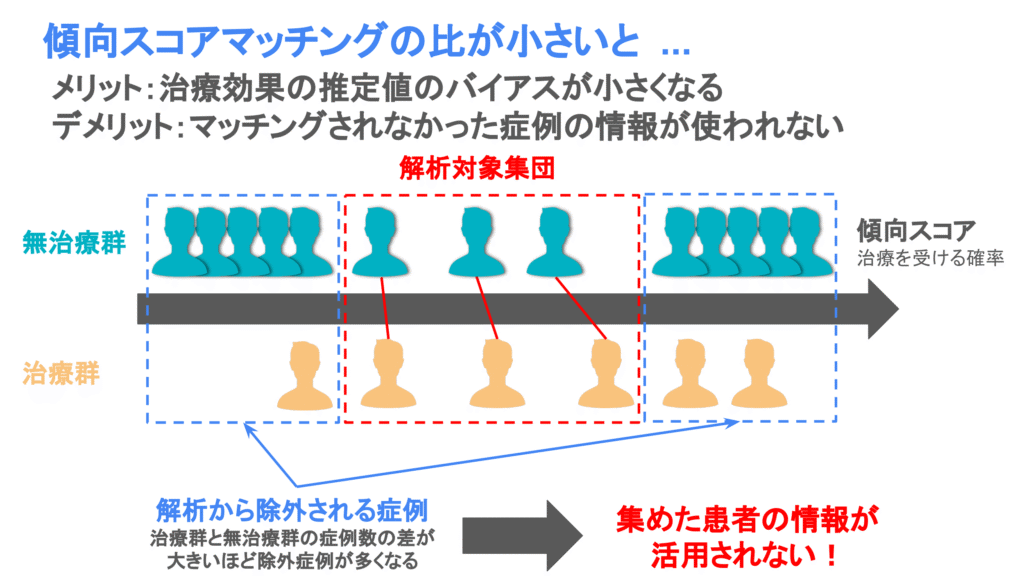
マッチング比率が小さい場合、マッチング対象が見つかりやすく、患者背景が揃いやすくなるというメリットがあります。また患者背景が揃うことにより、純粋な治療効果の推定が可能となり、推定値のバイアスが小さくなることが分かっています。

ただし、マッチング前のデータで２つの群の症例数に大きな偏りがある場合、片方の群の症例データの多くを解析から除外することになり、多くの患者データが活用されなくなるということには注意が必要です。例えば、治療群が100例、無治療群が1000例だった場合、1:1マッチングでは無治療群のデータのうち、900例分が使われないデータとなります。

そのため、マッチング前の症例数に偏りが大きい場合は、マッチング比率を大きくした傾向スコアマッチングも考えておく必要があります。

マッチング比率が大きい場合

マッチング比率が大きい場合、症例数が増えることで推定値の分散が減少し、推定精度が向上するというメリットがあります。これによって、信頼度の高い解析結果が得られる一方で、患者背景の偏りが制御できないなど、推定値が真の値よりも外れた値になるバイアスが入ることがあります。

そのため、治療効果をバイアスなく評価することがメインの目的である後ろ向き研究などでは、マッチング比率を大きくした解析が適していないとも考えられます。

最適なマッチング比率（1:1、1:2）でもマッチングの偏りをチェック！

最適なマッチング比率は1:1または1:2と言われていますが、1:1または1:2でのマッチングでも患者背景の偏りは忘れずに確認しておきましょう！

というのも、マッチングしたとしてもマッチング後の患者背景が整っていない可能性があるからです。特に傾向スコアの算出に使っていない因子は偏る可能性があります。

マッチングの偏りを確認する方法は大きく２つあります。

マッチングの偏りを確認する方法

ヒストグラムを描いて確認する
標準化差（standardized difference）を計算する

マッチングの偏りを確認する方法①：ヒストグラムを描いて確認する

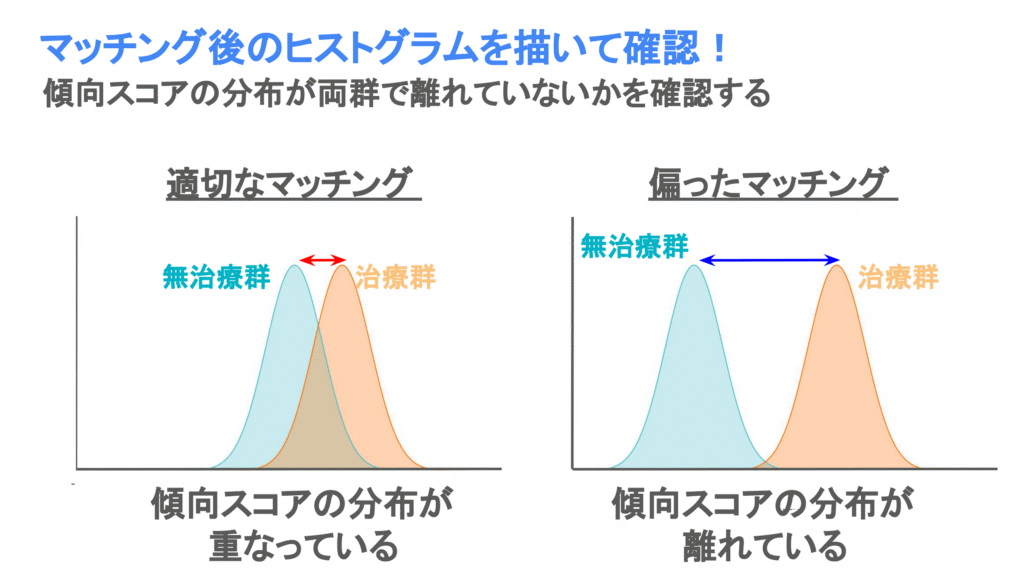
マッチング後の傾向スコアの分布が乖離していないかヒストグラムを描いて確認してみましょう！

もし２つの治療群のヒストグラムが重なっていれば、適切なマッチングがされています。逆にヒストグラムが離れている場合はマッチングが適切に行えていない可能性があります。

その場合はマッチング比を変更したり、キャリパー幅を調整して、マッチングをやり直しましょう。

マッチングの偏りを確認する方法②：標準化差（standardized difference）を計算する

患者背景が偏っていないかを確認するためにはよく標準化差（standardized difference）という指標が使われます。
標準化差はマッチング後の患者背景を標準化した、それらの差のことです。
標準化差の絶対値が0.1未満に収まっている場合には、マッチング後の背景は整っている、というように解釈できます。

標準化差（$d$）は以下のように計算することができます。

$d=\frac{治療群の平均値-無治療群の平均値}{\sqrt{(治療群の分散+無治療群の分散)/2}}$

検定を使って評価するのはどうなの？

患者背景の比較によく検定が使われているのを目にします。
では、その検定を使ってマッチング後の患者背景を比較して、マッチングの偏りを評価するのはどうでしょうか？

これは適切なマッチングの偏りの評価方法とは言えません！

というのも、検定で算出されるｐ値は症例数が多くなるほど小さくなることが分かっています。つまり、マッチング後にｐ値が大きくなったとしても、「本当に患者背景に差がないため、ｐ値が大きくなったのか」、「マッチングによって症例数が少なくなったため、ｐ値が大きくなったのか」を判断することができません。

そのため、マッチング後の患者背景の偏りを評価するために検定を用いるのは適切ではなく、標準化差を使って評価する必要があります。