複数の群でカテゴリカルデータを比較するときにはよくカイ二乗検定が使われます。
ただしカイ二乗検定には近似にズレが生じることが知られており、その結果計算の精度にバイアスが入る可能性があります。
そのため、そのズレを補正して正確な結果を得るための方法としてイエーツの補正という方法が使われています。
今回はイエーツの補正の詳細とイエーツの補正が使われる状況について解説します!
またEZRでのイエーツの補正を行ったカイ二乗検定の方法も解説していますので是非ご覧ください!
カイ二乗検定のイエーツの補正とは?

群間でカテゴリカルデータを比較するときにはよくカイ二乗検定が使われます。
イエーツの補正(Yates’ continuity correction)とはカイ二乗検定のうち、2×2の分割表に対するカイ二乗検定において計算過程に補正をかける方法です。
イエーツの補正が必要な理由はカテゴリカルデータから連続型の分布であるカイ二乗分布への近似には少しズレがあり、検定が有意になりやすいという問題があるからです。
一般に医学研究ではβエラーよりもαエラーを重視する傾向があります。
というのも、有効な治療を見逃すこと(βエラー)よりも無効な治療を有効と判定すること(αエラー)を抑えたいということです。
そのため、αエラーが過大にならないように制御するイエーツの補正が使われています。
補足:離散型を連続型で扱うとは?
カイ二乗検定は離散型であるデータを連続型のカイ二乗分布に近似して検定を行っています。この離散型を連続型として扱うとはどういう意味でしょうか?
例えば、男性・女性のようなカテゴリーに分けられる離散型のデータを考えます。このような離散型データを連続値として扱うというのは、男性を1、女性を2としたときに「0.5や1.5のときの性別は?」と定義できないカテゴリーを定義するということになります。これは本当に妥当な定義でしょうか?
イエーツの補正の計算方法

通常のカイ二乗検定では、カイ二乗値はセルごとの観測データと期待データの差の二乗を期待度数で割った値の和として計算されます。
$\frac{|観測度数-期待度数|^2}{期待度数}$
イエーツの補正では、セルごとの観測データと期待データの差から0.5を引いた値の二乗を期待度数で割った値を足し合わせてカイ二乗値を計算します。
$\frac{(|観測度数-期待度数|-0.5)^2}{期待度数}$
例えば以下のようなデータでイエーツの補正なしとありの場合の計算方法を見ていきましょう!
| 治療効果なし | 治療効果あり | 合計 | |
|---|---|---|---|
| 治療A | 30 | 30 | 60 |
| 治療B | 15 | 25 | 40 |
まず期待度数を計算していきます。期待度数は、そのセルの(行の確率)*(列の確率)*(試行回数)で計算できます。そのため、期待度数は以下のような値になります(例えば左上のセルであれば、60/100 * 45/100*100=27と計算されます)。
| 治療効果なし | 治療効果あり | 合計 | |
|---|---|---|---|
| 治療A | 27 | 33 | 60 |
| 治療B | 18 | 22 | 40 |
次にセルごとの観測度数と期待度数を使ってカイ二乗値を計算していきます。補正なしと補正ありではそれぞれ以下のように計算できます。
| セルの位置 (群, 治療効果) | イエーツの補正なし | イエーツの補正あり |
|---|---|---|
| 左上(群1, なし) | $|30-27|^2/27≒0.33$ | $(|30-27|-0.5)^2/27≒0.23$ |
| 右上(群1, あり) | $|30-33|^2/33≒0.27$ | $(|30-33|-0.5)^2/33≒0.19$ |
| 左下(群2, なし) | $|15-18|^2/18=0.50$ | $(|15-18|-0.5)^2/18≒0.35$ |
| 右下(群2, あり) | $|25-22|^2/22≒0.41$ | $(|25-22|-0.5)^2/22≒0.28$ |
| 和(カイ二乗値) | 1.5 | 1.1 |
| p値 | 0.2184 | 0.3050 |
イエーツの補正なしとイエーツの補正ありのカイ二乗値を比較すると、イエーツの補正ありの方が小さくなっていることが分かります。つまり、p値が小さくなり有意になりにくくなる、ということになります。
イエーツの補正はいつ必要?

イエーツの補正はどんな時に必要でしょうか?
ズバリ!イエーツの補正が必要と考えられるのは各セルの症例数が少ないときです!
多くの場合は期待度数が5を下回る場合にはイエーツの補正が必要とされています。
というのも、上の計算方法でも分かるようにイエーツの補正はカイ二乗値の計算時に0.5を引いているだけです。つまり、各セルの度数が多いときには0.5という補正は無視できるため、無視できない程度の症例数のときは必要ということです。
EZRでイエーツの補正の影響を確認しよう!

イエーツの補正を行ったカイ二乗検定をEZRで行ってみましょう!
使用するデータ
使用するデータは以下の治療Aと治療Bの治療効果の頻度を比較するのデータです。
例えば、がんの臨床試験において、2つの治療効果を奏効率を使って比較する場合が考えられます。
| 治療効果なし | 治療効果あり | 合計 | |
|---|---|---|---|
| 治療A | 30 | 30 | 60 |
| 治療B | 15 | 25 | 40 |
EZRでイエーツの補正ありのカイ二乗検定をやってみよう!
カイ二乗検定は[統計解析]→[名義尺度の解析]→[分割表の作成と群間の比率の比較(Fisherの正確検定)]から行うことができます。
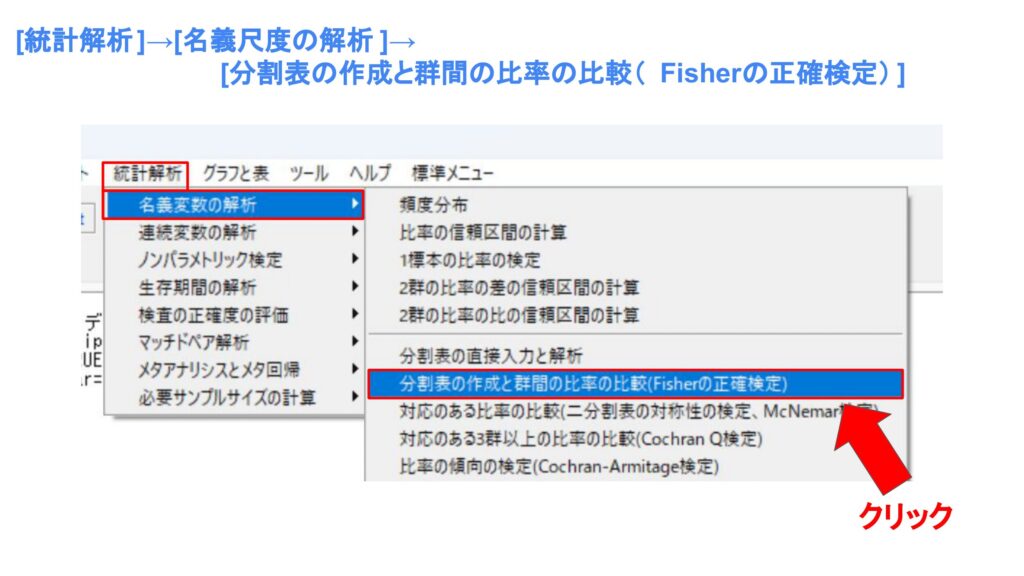
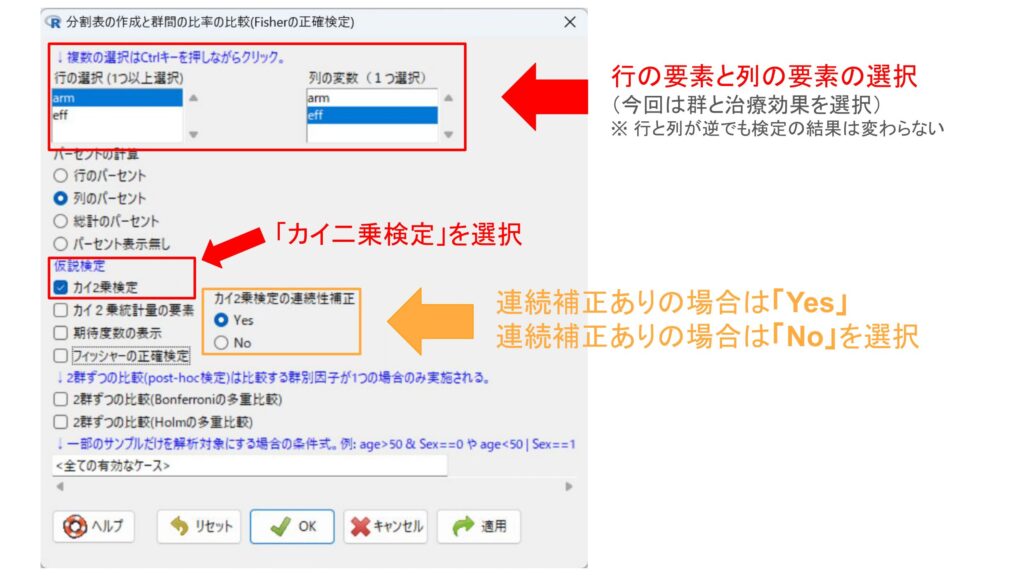
すると以下のようなウィンドウが開くので、「行の選択」と「列の選択」から行と列の変数を選択します。
イエーツの補正の有無はオレンジの枠から選択することができます。イエーツの補正ありの場合は「Yes」、イエーツの補正ありの場合は「No」を選択します。
イエーツの補正なしとありの場合のカイ二乗検定検定の結果の違い
実際にイエーツの補正なしとありの場合のカイ二乗値とp値は以下のようになります。イエーツの補正なしの場合のp値は0.2184、イエーツの補正ありの場合のp値は0.3050と、イエーツの補正を使った方がp値が大きくなっていることが分かります。

まとめ

今回はイエーツの補正について解説しました!
カイ二乗検定は離散型データを比較するときに離散型のデータを連続値のカイ二乗分布に近似して比較する方法です。
ただカイ二乗検定での近似には少しのズレがあり、p値が小さくなり、有意になりやすいという特徴がありました。また被検者保護の観点からは有意になりやすくなり、αエラーが増大することは避けなければいけません。
そんなときに役立つのがイエーツの補正です。イエーツの補正は少し割り引いてカイ二乗値を計算することで、αエラーが増大することを抑制します。
特に症例数が少ないときはイエーツの補正によって検定結果の信頼度が増しますので、ぜひ覚えておきましょう!





コメント