医学研究で避けられない取り扱いに困るデータとして「外れ値」があります。
外れ値の多くはヒューマンエラーにより発生します。
外れ値を取り扱うときには常に解析から除外していないでしょうか?
外れ値は常に除くのではなく、場合によって取り扱い方が変わってきます。
この記事では外れ値の検出方法と取り扱い方法を解説します!
外れ値の定義と原因

外れ値とは「臨床的に通常取りえない値や他のデータから極端に外れた値」のことです。
外れ値が発生する原因は数々ありますが、代表的な例として以下が挙げられます。
外れ値が発生する原因
- 小数点の間違い(1.23を12.3と入力)
- 測定単位の認識違い(gをkgで入力)
- 特別な背景の症例が含まれる
「小数点の入力間違い」や「測定単位の認識違い」はヒューマンエラーになりますので、データ入力の際には注意することで、外れ値を防ぐことができます。
「特別な背景の症例が含まれる」場合には、そのデータは間違いではありませんが、どうして外れた値になっているか、を調べる必要があります。
その理由によって、解析から除くべきか含めてもよいかの判断を行います。
外れ値を検出する方法

外れ値を検出するにはグラフを使うのが最も有効です。
例えば、外れ値が含まれる場合と含まれない場合のグラフ(箱ひげ図とヒストグラム)を見てみましょう!
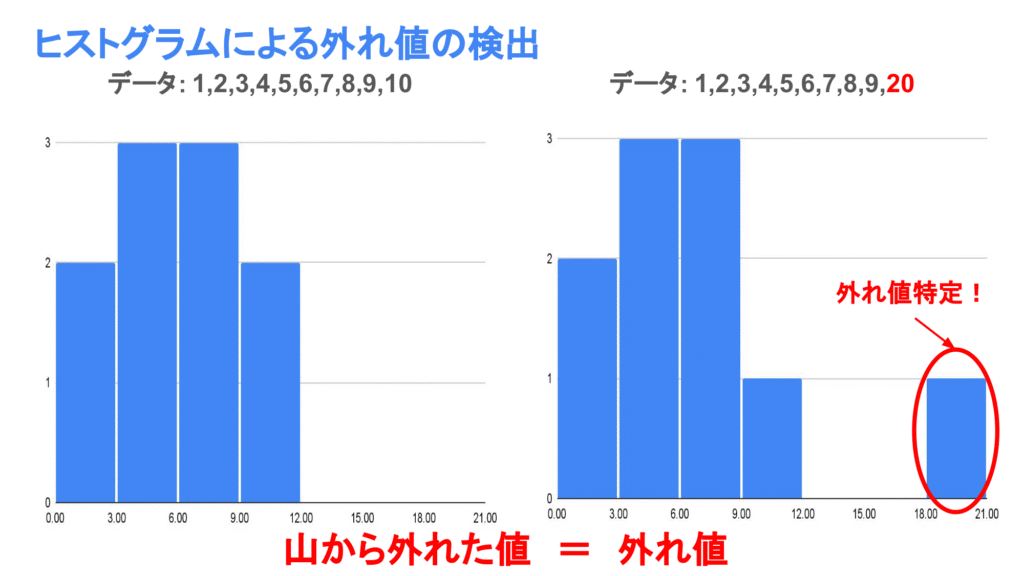
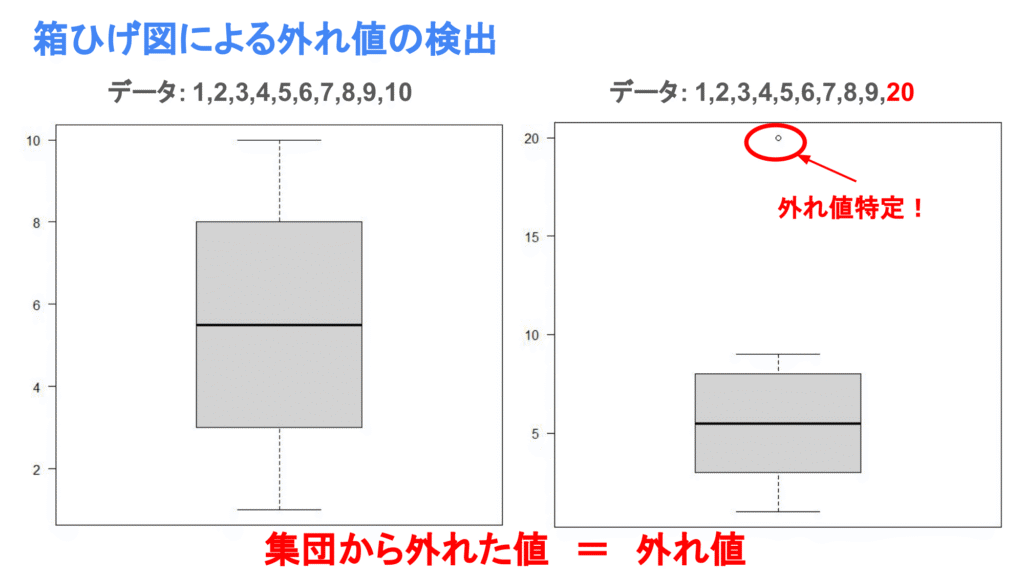
グラフを描くことで集団から離れた値が一目瞭然となり、この集団から離れた値が外れ値になります。
グラフを使う方法以外にもスミルノフ・グラブス(Smirnov-Grubbs)検定や平均値から標準偏差の3倍以上離れた値で判断することもあります。ただし、これらの方法は症例数に依存するため、これらのみで判断することは推奨されません。
また、グラフや検定によって外れ値だと判断するだけでも不十分です。
というのも、集団から離れていたとしても、臨床的に妥当な値である可能性があるからです。
そのため、外れ値を検出する際は、グラフを描いて外れ値の候補を特定しつつ、臨床的にありえない値かどうかで判断しましょう!
外れ値があると結果に影響がある!

データに外れ値がある場合、データの要約方法によって結果に影響を及ぼすことがあります。
特に平均値や回帰モデルを使って解析を行った場合には誤った結果にミスリーディングしていしまうことがあります。
これら二つの例について見ていきましょう!
平均値への影響
平均値は外れ値の影響を受けやすい指標です。
例えば、以下二つのデータで平均値を計算してみましょう!
データ1:1, 2, 3, 4, 5, 6, 7, 8, 9, 10
データ2:1, 2, 3, 4, 5, 6, 7, 8, 9, 20
データ1には外れ値が含まれていませんが、データ2には20という外れ値が含まれています。
これらで平均値を計算すると、データの1平均値は5.5、データの2平均値は6.1になります。
このように平均値は外れ値に引っ張られてしまうので、外れ値が含まれているかいないかで解釈が変わりえます。
回帰モデルへの影響
外れ値が含まれている場合、回帰モデルの推定値に影響があります。
例えば、以下の例では1つの集団とそこから外れた外れ値がある場合の散布図を示しています。
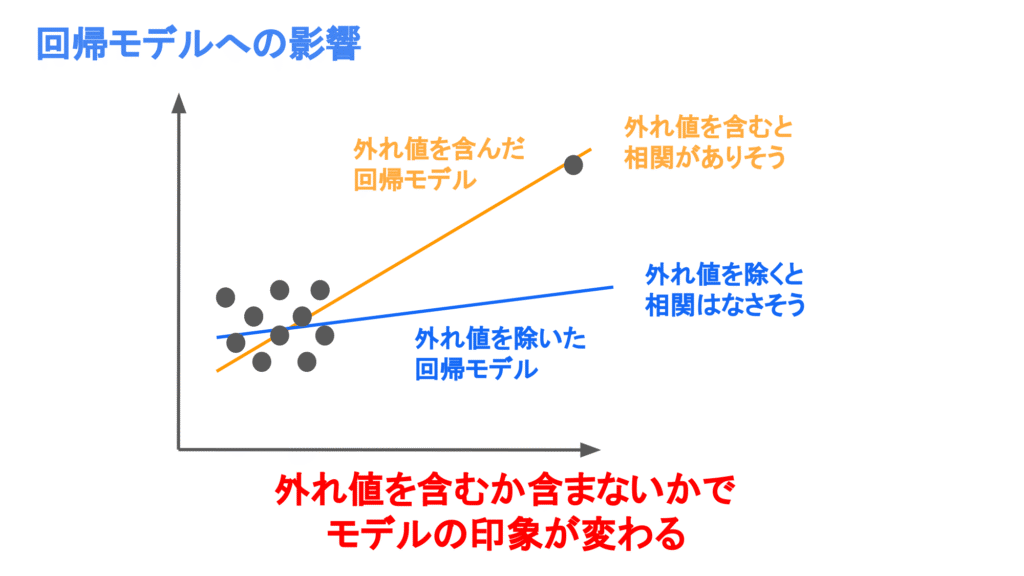
このデータに回帰モデルを引いてみると、外れ値がある場合、外れ値に引っ張られて傾きが大きくなり相関があるように見えます。
一方で、外れ値を除くと傾きが小さくなり、二つのデータは無関係のように見えます。
そのため、外れ値が含まれていることで見かけの相関が現れてしまい、解釈が変わってしまいます。
外れ値があるときの対応と解析方法

では、外れ値がある場合にはどのように対応すればよいでしょうか。
ここでは、代表的な2つの対応を見ていきましょう!
外れ値があるときの対応と解析方法
- 外れ値を除外して解析する
- 外れ値に影響されにくい解析方法を使う
外れ値を除外して解析する
一番シンプルな方法が外れ値を除外して解析する方法です。
例えば、以下のデータでは20が外れ値であるため、20を除外して解析を行います。
データ:1, 2, 3, 4, 5, 6, 7, 8, 9, 20
こうすることで外れ値が含まれたデータでは平均値が6.1であるのに対して、外れ値を除くと平均値は5.0となり、外れ値の影響を除くことができます。

ただし、外れ値を除外するときには、臨床的に除いていいデータかを事前に判断する必要があります。
また、感度解析として外れ値を含めた場合の解析を行って、外れ値がどのように影響しているか確認することも大切です!
外れ値の影響を受けにくい解析方法を使う
2つ目の方法が外れ値の影響を受けにくい解析方法を使う、ということです。
外れ値の影響を受けにくい解析方法として、平均値の代わりに中央値を使うことやt検定の代わりにウィルコクソン検定を使うことなどが挙げられます。
例えば、以下のデータで平均値と中央値を計算すると平均値は6.1であるのに対して、中央値は5.5となり、集団を代表する値として妥当な値となります。
データ:1, 2, 3, 4, 5, 6, 7, 8, 9, 20

また検定方法としてt検定のように値をそのまま利用して検定を行う方法より、データを順序データに直して検定を行うウィルコクソン検定の方が外れ値の影響を受けにくくなっています。
まとめ

今回は外れ値の検出方法と外れ値が含まれているときの解析方法を解説しました!
外れ値を検出するためにも、解析前にはヒストグラムなどでデータの分布を確認するようにしましょう。
外れ値には集団から外れていても、臨床的に妥当な値である場合があるので、
単に「集団から離れた値=外れ値」ではなく、臨床的に外れ値とするかどうかの判断をしましょう!





コメント