医学研究ではよくレビュアーからデータが正規分布に従っているか調べるように指摘されることがあります。その際に使われるのが、正規性の検定です。
正規性の検定では二者択一で「データが正規分布に従っているか」を調べられるため、解釈がしやすく非常に便利な方法です。
ただ正規性の検定のみの検証には大きな落とし穴があります!
今回は正規性の検証が不要であると考える理由と、それでも正規性の確認は役に立つ理由について解説します!
正規性の検定とは?

正規性の検定とはデータが正規分布に従っているかを調べる検定のことです。つまり、データが左右対称の釣鐘型になっているか、ということを確認します。
正規性の検定の帰無仮説と対立仮説は以下のように設定されます。
- 帰無仮説:データが正規分布に従う
- 対立仮説:データが正規分布に従わない
そのため、正規性の検定のp値が小さくなればデータは正規分布に従わないと判断します。
正規性の検定方法には以下のような方法があります。
正規性の検定の例
- Shapiro-Wilk検定(シャピロ-ウィルク検定)
- Kolmogorov-Smirnov検定(コルモゴロフ-スミノフ検定)
どの方法を使っても同じく「データが正規分布に従っているか」を調べますが、症例数によっては制度が悪くなる場合もあるため注意が必要です。
正規性の検定が不要な理由

正規性の検定はデータが正規分布に従うかを二者択一で決めることができるため、非常に便利な検定に思えます。ではなぜ正規性の検定が不要と考えられるのでしょうか?
以下では大きく2つの点で不要と考える理由を説明します。
正規性の検定のp値は症例数に依存する
正規性の検定ではp値が有意水準より小さくなれば、データが正規分布に従わないと判断します。
ただp値は症例数に依存することが分かっています。p値と症例数の関係は一般に症例数が多くなればp値は小さくなり、症例数が少なければp値は大きくなります。
そのため、真にデータが正規分布に従っていたとしても、症例数が多くなればデータは正規分布に従わないと判断しやすくなります。
このように正規性の検定は症例数に依存して判断が変わり、解釈不能となることが多々あるため、不要であると考えられます。
検定の多重性の問題
多くの場合、正規性の検定は特定の一つの項目だけでなく、複数の項目に対して行われます。例えば、「身長が正規分布に従うか」だけではなく、体重、血圧、血中濃度…と複数の項目に関して、正規性の検定が行われます。
このように検定を複数回行うと検定の多重性が問題となります。
検定の多重性というのは、検定を複数行うとαエラーが増大する、という問題です。つまり、すべてのデータが正規分布に従っていたとしても、たまたまの偶然でいずれかのデータが「正規分布に従っていない」と判断されることになります。
このような検定の多重性が問題となる中では、正規性の検定による結果のどれが正しいのか判断がつかなくなり、検定の結果の解釈が困難となります。
それでも正規性を調べることが役に立つ理由

正規性の検定は不要であると考えられますが、正規性を調べることは非常に役に立つ作業です。というのも、解析方法の多くは正規分布を前提としています。例えばt検定は正規分布に近いt分布を前提にした検定方法です。
正規性を調べておけば、もし正規分布を前提とした解析を行って、うまく効果を推定できなかったり、実臨床の感覚と大きくずれたりしたときに、上手くいかなかった理由が正規性ではないかと確認することができます。また正規分布に従った解析ではなく、分布を前提としないノンパラメトリックな解析を選択する、というように適切な解析方法の選択にもつながります。
そのため、データが正規分布に従っているかを正規性の検定のみに頼るのは勧められませんが、多角的に正規分布に従っているか、を調べることは重要な作業になります。
検定に頼らない正規性の確認方法

では検定による正規性の確認が推奨されないのであれば、どのようにして正規性を確認すればよいでしょうか?
正規性を確認する方法としてグラフィカルな方法があります。
正規性を確認するグラフィカルな方法
- ヒストグラム
- Q-Qプロット
以下ではこれら2つのグラフィカルな方法について見ていきましょう!
ヒストグラム(Histogram)
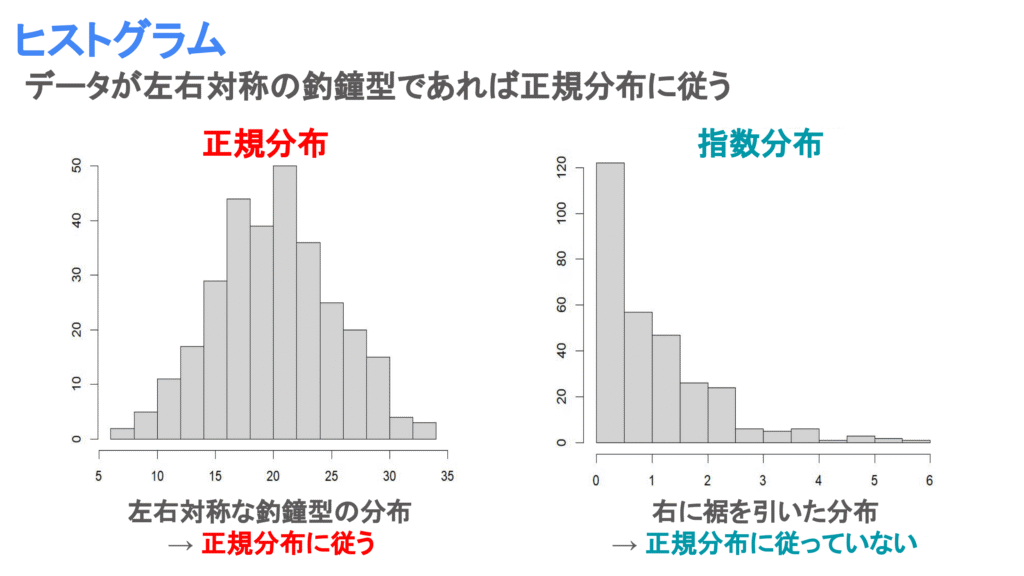
一番シンプルな方法はヒストグラム(Histogram)を描くことです。ヒストグラムはデータを小さい順に区切って、その区間に含まれるデータ数を棒グラフ状に示したグラフです。
ヒストグラムが左右対称な釣鐘型であれば正規分布に従っていることが考えられます。
Q-Qプロット(quantile-quantile plot)
正規分布の他にはよくQ-Qプロット(quantile-quantile plot)と呼ばれるグラフが使われます。Q-Qプロットは名前の由来の通り、パーセント点を使ったグラフです。
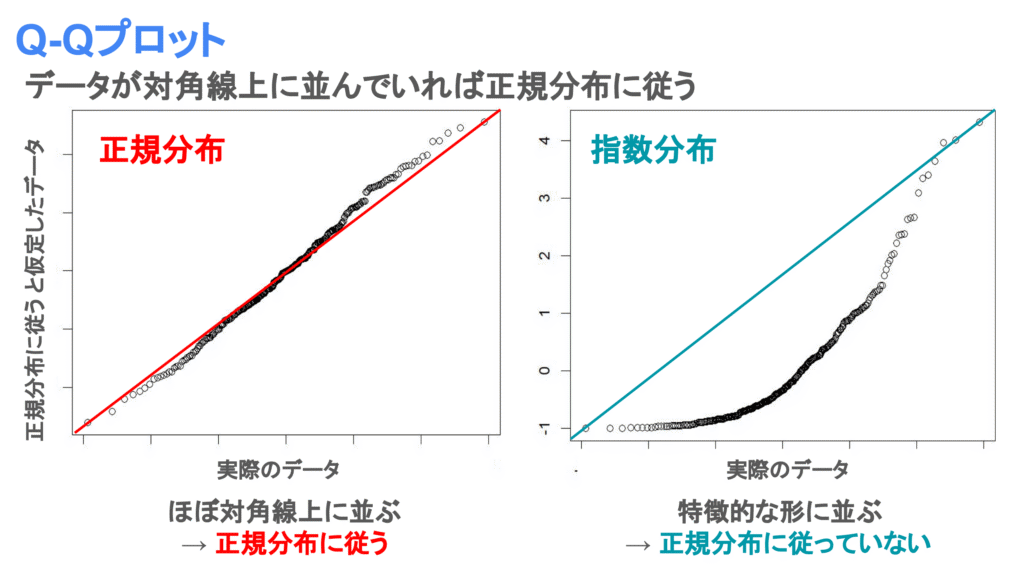
グラフの描き方の詳細は割愛しますが、横軸に小さい順に並べた各実データ、縦軸に正規分布に従うと仮定した時の理想データをプロットして作成します。
Q-Qプロットは以下のような図で、プロットが対角に並んでいるとき、データが正規分布に従っていると考えられます。(左図:実データが正規分布に従う、右図:実データが指数分布に従う)
どの程度対角に並んでいれば正規分布に従っているかという基準はありません。ただ指数的に増加するなど特徴的な形で並んでおらず対角に並んでいるのであれば、データが正規分布に従っていると考えてよいでしょう。
まとめ

今回は正規性の検定がなぜ不要な理由とそれでも正規性を確認することの意義について解説しました!
正規性の検定は事後的な解析となることが多く、症例数とp値の関係や検定の多重性が問題となるため、推奨することはできません。
ただ正規性を検証することには意味があり、適切な解析手法の選択にもつながります。
そのため、正規性を確認する際には、正規性の検定だけに頼るのではなく、ヒストグラムやQ-Qプロットなどグラフィカルな方法で正規性を確認するようにしましょう!






コメント