カテゴリカルデータを比較するときによくカイ二乗検定が使用されます。
カイ二乗検定はよく使われる検定方法ですが、何をどのように比較しているのか、理解できていますでしょうか?
今回はカイ二乗検定の中でもよく使用される適合度検定と独立性の検定の詳細と使い方について解説します!
またExcelでの計算例や簡単な計算ツールも用意していますので、ぜひ参考にしてみてください!
カイ二乗検定はカテゴリカルデータを比較する検定

カイ二乗検定はカテゴリカルデータの比較に使われる検定方法です。
カテゴリカルデータは治療効果のあり/なしのように、いくつかのカテゴリに分割され、度数や割合で評価されるデータのことです。
カイ二乗検定はこのカテゴリカルデータにおいて、
「想定した割合と差があるか」や「群間で割合に差があるか」を調べます。
カイ二乗検定の手順はt検定などの他の検定の手順と同じです。
具体的には以下の手順で進めます。
カイ二乗検定の手順
- 帰無仮説を立てる
- 有意水準を決める
- 検定統計量(カイ二乗値)を計算する
(期待度数を計算する必要あり!) - p値を計算する
- p値と有意水準を比較する
代表的なカイ二乗検定の種類:適合度検定と独立性の検定

カイ二乗検定は大きく2種類の方法で使われます。
カイ二乗検定の種類
- 適合度検定:単群で想定した割合と差があるか
- 独立性の検定:多群の各カテゴリーの割合に差があるか
主に適合度検定は単群で、独立性の検定は多群で使用されます。
そのため、想定している確率との比較に興味があるのか、群間での割合の差に興味があるのか、によって、検定の記載は使い分けましょう。
以下では適合度検定と独立性の検定の具体的な方法と解釈を説明します!
適合度検定(goodness of fit test)
適合度検定は1つの群において観測された割合が想定していた割合と同じかを調べる検定です。
帰無仮説と対立仮説は以下のように設定します。
適合度検定の帰無仮説と対立仮説
- 帰無仮説:観察された割合は想定していた割合と同じ
- 対立仮説:観察された割合は想定していた割合と差がある
適合度検定では、観察されたデータと期待しているデータがどれぐらい乖離しているかを調べて、差があるかどうかを判断します。
以下の2つの例を使って適合度検定で何を調べているのか実際に見ていきましょう!
- サイコロの各目が出る確率は全て同じ?
- 治療効果があった患者割合は想定していた30%と同じ?
サイコロの各目が出る確率は全て同じ?
偏りのないサイコロではどの目も1/6の確率で出ることが想定されます。
もし120回サイコロを振って、以下のようなデータが得られたとき、
このサイコロはどの目も等しく1/6の確率で出ると言えるでしょうか?
これを調べることができるのが適合度検定で、帰無仮説を「サイコロのどの目も出る確率は1/6」と設定して、サイコロの目がどれも1/6で出るかを調べます。
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 | 合計 |
|---|---|---|---|---|---|---|---|
| 観測度数 | 15 | 23 | 22 | 18 | 25 | 17 | 120 |
| 期待度数 | 20 | 20 | 20 | 20 | 20 | 20 | 120 |
これを調べるには、最初に「サイコロのどの目も出る確率が1/6だったとき、期待される各目が出る回数」を計算します。
これを期待度数と呼びます。
今回は120回振って各目が1/6の確率で出るので、期待される各目が出る回数は120*1/6=20回となります。
適合度検定ではこの期待度数と観測される度数を比較して、観察されたデータが期待されるデータと乖離しているかを調べます。
実際に計算してみると、カイ二乗検定の検定統計量は3.8、p値は0.5786となります。もし有意水準5%であれば、帰無仮説は棄却されず、「サイコロのどの目も出る確率は1/6」と判断されます。
治療効果があった患者割合は想定していた30%と同じ?
次は臨床研究を題材に適合度検定を見ていきましょう!
例えば、患者にある治療を行ったとき、得られた結果が過去の臨床研究などから想定される治療効果と同じかどうかを調べたいとします。このとき、想定している治療効果を30%とします。
10例の患者を治療して、以下のようなデータが得られたとき、治療効果は想定している治療効果の30%と同じと言えるでしょうか?
これを調べるために適合度検定が用いられます。
今回適合度検定の帰無仮説は「治療効果は30%と等しい」、対立仮説は「治療効果は30%と等しくない」が設定されます。
| 治療効果なし | 治療効果あり | 合計 | |
|---|---|---|---|
| 観測度数 | 6 | 4 | 10 |
| 期待度数 | 7 | 3 | 10 |
適合度検定では初めに帰無仮説が正しいとき、つまり「治療効果が30%」だったときに期待されるデータを計算します。今回は10例治療しているので、期待される治療効果ありの症例は10*0.3=3例、期待される治療効果なしの症例は10*(1-0.3)=7例ということになります。
この期待されるデータと観測したデータの差を使って、「得られたデータが想定と同じか」を調べていきます。
今回の期待されるデータと観測したデータを使って計算してみると、カイ二乗値は4.3となり、p値は0.0384となります。もし有意水準が5%であれば、帰無仮説は棄却され、「治療効果は30%と等しくない」と判断されます。
独立性の検定
独立性の検定は、多群においていずれかの群でカテゴリの発生割合に差があるかどうかを調べる検定です。
独立性の検定では
帰無仮説は「いずれの群もカテゴリの発生割合は同じ」、
対立仮説は「いずれかの群でカテゴリの発生割合に差がある」
と設定されます。
例えば、治療Aと治療Bと治療Cの治療効果が「あり or なし」の二つのカテゴリで評価される場合、治療Aと治療Bと治療Cの治療効果は同じなのか、どこかの群で治療効果に差があるのかを調べます。
注意が必要なのは、独立性の検定で分かることは、「どこかの群に差がある」ということだけであること。
つまり、「治療効果が高いのはどの群か」ということは分かりません。
もしどの群で治療効果が高いかを調べたいときは、Tukey検定のような多重性を調整した解析を用いましょう。
実際に独立性の検定の手順を見ていきましょう!
簡単にするために、治療Aと治療Bの2つの治療の治療効果が「あり or なし」の二つのカテゴリで評価される場合を考えましょう。
各治療でそれぞれ20例の治療を行って、得られた結果が以下であるとします。
この結果から治療Aの治療効果は50%、治療Bの治療効果は62.5%になります。
このとき、「治療Aと治療Bの治療効果は同じ」と言えるでしょうか?
これを調べるのが独立性の検定になります。
| 治療効果なし | 治療効果あり | 合計 | |
|---|---|---|---|
| 治療A | 20 | 20 | 40 |
| 治療B | 15 | 25 | 40 |
実際に独立性の検定を行うと、カイ二乗値は1.27、p値は0.2598となります。有意水準が5%であれば、帰無仮説は棄却されず、「治療Aと治療Bの治療効果に差はない」と判断されます。
カイ二乗検定は両側検定?片側検定?

よくカイ二乗検定を使って「治療効果が想定より高かった」や「治療Aよりも治療Bの方が治療効果が高かった」と言ってよいか?と質問されることがあります。つまり、片側検定の解釈をしてもよいか?と聞かれます。
答えはNoです。
カイ二乗検定は両側検定です。
帰無仮説を見ても、適合度検定は「想定していた割合と比べて差がない」、適合度検定は「いずれの群も割合に差がない」というように「差があるかないか」という点に注目しています。
そのため、カイ二乗検定は両側検定であり、
検定で有意差があったとしても主張できるのは「差があった」ということのみです。
もしカテゴリカルデータの比較で片側検定を行いたいのであれば、正確検定やFisherの直接確率検定を用いるのがよいでしょう。(カイ二乗値でも片側検定はできますが今回は割愛…)
Excelでカイ二乗検定をやってみよう!計算ツールの配布も!

カイ二乗検定はExcelで簡単に計算することができます。
適合度検定でも独立性の検定でも使う関数は「CHITEST関数」です。
CHITEST関数ではデータを以下のように指定します。
=CHITEST(観測度数, 期待度数)
CHITEST関数を用いる上で注意が必要なのは、「期待度数は自分で計算する必要がある」ということです。
期待度数の計算方法は適合度検定と独立性の検定でが異なるので順番に見ていきましょう!
一番シンプルな例で計算できるツールも以下からダウンロードできるので、是非参考にしてみてください!ツールは自動で期待度数の計算もできます。
適合度検定
適合度検定では、期待度数を(各カテゴリが発生する期待確率)*(試行回数)で計算します。
例えば、サイコロの目がどれも1/6で出ることを調べたいのであれば、期待度数は1/6*(試行回数)で計算されます。
例えば、以下のような場合で適合度検定のp値を計算してみましょう!
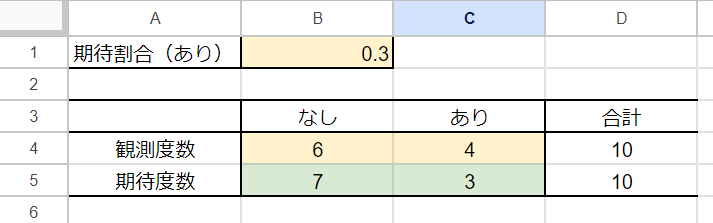
「あり」の期待割合を30%、試行回数を10回と設定すると、
期待度数はそれぞれ「なし」が10*(1-0.3)=7、「あり」が10*0.3=3になります。
これを計算した上で、以下のように関数に入れることで、独立性の検定のp値は0.4902と計算されます。
=CHISQ(B4:C4, B5:C5)
独立性の検定
独立性の検定では、期待度数を各セルごとに計算します。
期待度数は計算したいセルの(行の確率)*(列の確率)*(総数)で計算されます。
少しわかりにくいので、数値を使って計算していきましょう!
今回使用するデータは以下のデータです。
| 治療効果なし | 治療効果あり | 合計 | |
|---|---|---|---|
| 治療A | 30 | 30 | 60 |
| 治療B | 15 | 25 | 40 |
まず行の確率と列の確率をそれぞれ計算します。
行の確率は全ての群をあわせたときの治療Aと治療Bの患者割合のことを指します。
実際に行の確率を計算すると、治療Aの確率は60/100=0.6、治療Aの確率は40/100=0.4となります。
同様に列確率は全ての群をあわせたときに治療効果なし/治療効果ありとなった患者の割合です。
実際に計算すると、治療効果なしの確率は45/100=0.45、治療効果ありの確率は55/100=0.55となります。
これらの行の確率と列の確率を使って、各セルの期待度数を計算していきます。
期待度数はセルごとに計算して、そのセルの(行の確率)*(列の確率)*(総数)で計算できます。
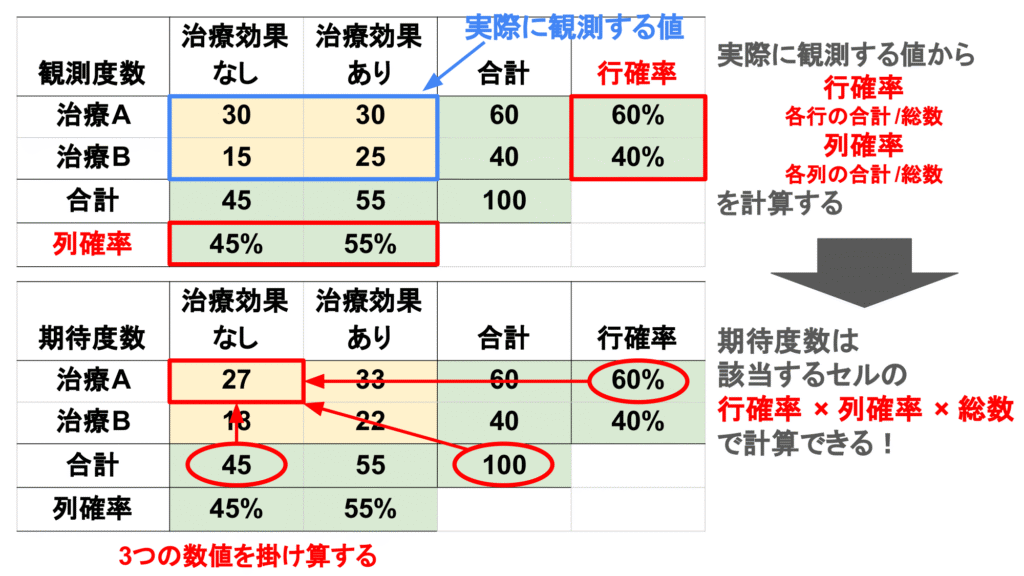
今回の例で各セルの期待度数を計算すると以下のようになります。
- 左上のセル(治療Aかつ治療効果なし):0.6*0.45*100 =27
- 右上のセル(治療Aかつ治療効果あり):0.6*0.55*100 =33
- 左下のセル(治療Bかつ治療効果なし):0.4*0.45*100 =18
- 右下のセル(治療Bかつ治療効果あり):0.4*0.55*100 =22
これらの情報を使って適合度検定の検定統計量を計算します。
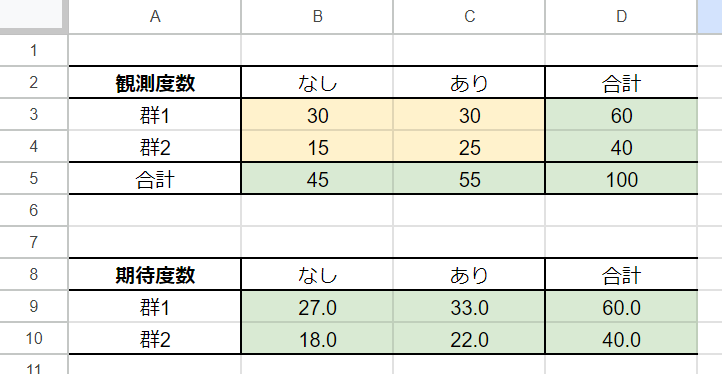
実際にExcelに入力すると以下のような形になり、カイ二乗検定のp値は
=CHITEST(B3:C4,B9:C10)
と指定することで計算することができます。
CHITEST関数を使って独立性の検定のp値を検定すると0.2184になります。
まとめ

今回はカテゴリカルデータを比較する検定方法であるカイ二乗検定について解説しました!
カイ二乗検定がよく使われる検定方法として、適合度検定と独立性の検定があります。
それぞれ以下のような違いがあるので、ぜひ記事を参考に使い分けてください!
カイ二乗検定の種類
- 適合度検定:想定した割合と差があるか
- 独立性の検定:多群の各カテゴリーの割合に差があるか





コメント