
群間で治療効果や患者背景に違いがあるか調べるとき、検定を使って調べることが多いと思います。この時何度も何度も検定を行っていないでしょうか?実は検定を繰り返して群間比較するのは、統計学的にNGなのです!
この記事では検定を繰り返すことで起こる検定の多重性の問題について説明します!よくある後ろ向き研究のときの問題についても解説しているので参考にしてください!
要約
- 検定を繰り返すことで研究全体のαエラーが有意水準を超えてしまう
- 検証的な研究では各検定の有意水準を調整することでαエラーを調整可能
- 各検定の有意水準を調整することが難しいときは効果量で報告するのがbetter!
仮説検定の復習
まず初めに仮説検定について復習しましょう。「2つの治療の治療効果に差があるか?」を調べたいとき、仮説検定は以下の手順で行っていました。

検定の多重性で問題となるのは、有意かどうかを判断する「有意水準」、ひいては有意水準と関連する「差がないときに誤って差があるといってしまう間違い」であるαエラーです。有意水準は別の言い方をすると「本当は差がないときにどれだけ間違って差があるといっていいか」という規準です。つまり、有意水準5%というのは、「本当は差がない母集団から100回ランダムに対象を選んできて検定を行ったら、5回は誤って差があるといってしまうことを許容する」ということになり、αエラーは5%まで許容するということになります。
検定を繰り返すとどうなるか?
では検定を繰り返すとαエラーはどうなるでしょうか?結論から言うと、検定を繰り返すとαエラーは事前に定めた有意水準よりも大きくなってしまいます!
実際に検定を繰り返したときのαエラーを見ていきましょう。例えば有意水準を5%として検定を2回行ったとします。2回の検定ともに帰無仮説が正しい時、各検定を有意水準5%で行うと、全体のαエラーは「いずれかの検定で有意になる確率=1-いずれの検定でも有意にならない確率」なので、1-(1-0.05)^2 = 0.0975 になり、最初に決めていた有意水準の0.05よりも大きくなってしまいます!

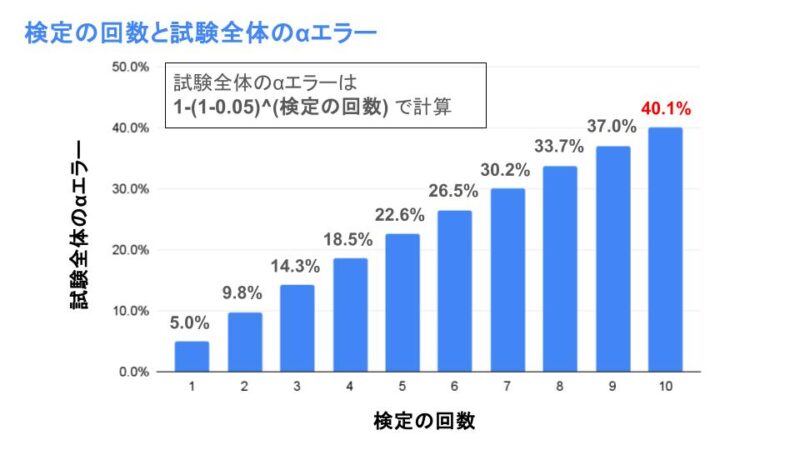
この全体のαエラーは検定の回数を増やすほど多くなり、有意水準5%のときの検定の回数と全体のαエラーは以下のようになります。10回も検定を繰り返せば試験全体のαエラーは40%(!!)を超えてしまいます!
検定を繰り返すことが妥当な場合
ただし常に検定を繰り返すことがNGということではありません。例えば前向き研究では事前に中間解析といってデータが全部集まる前に一部のデータで解析をするということがあります。このような中間解析では検定を繰り返しても事前に定めた有意水準を超えないような有意水準を使って解析することがあります。一番有名かつシンプルな方法はボンフェロー二(Bonfferoni)の方法で、この方法は各検定を試験全体の有意水準を検定の回数で割った有意水準で行う、という方法です。例えば試験全体の有意水準を5%として2回検定する場合、各検定の有意水準を5%/2回=2.5%として検定を行います。こうすることで試験全体のαエラーは1-(1-0.025)^2 = 0.049375(約4.9%)となり、事前に定めた5%を超えないということになります。
このように前向き研究では検定を繰り返す際には事前に各検定の有意水準をどのように決めるかを定めておくことで、検定の多重性の問題を解決しています。
後ろ向き研究の場合は?
では事前に解析方法を決めない後ろ向きの研究ではどうでしょうか?そもそも多くの後ろ向き研究は次の研究の参考にするような探索的な研究です。探索的な研究では多くの解析を行って検討を重ねながら、多角的な視点で治療効果や予後因子などを調べる必要があります。場合によっては「これも調べたい」と途中で検定の回数が増えることだってあります。
そのため、事前に検定の回数や解析方法を定めておくことは難しく、有意水準を調整すること自体が現実的ではありません(もし患者背景も含めて100回検定したら一回の検定の有意水準は5/100=0.05%!)。
「検定がなかったら差があるか判断できないよ!」という声が聞こえてきそうですが、その心配はありません!このような後ろ向き研究では検定ではなく、平均値や中央値といった要約統計量やオッズ比やハザード比といった指標、その精度を保証する95%信頼区間を使って評価するのが正しい研究報告の方法なのです!
例えばオッズ比やハザード比が1に近ければ、「治療効果に差はなさそうだ」とか、1から離れていれば「治療効果に差がありそうだ!」とまとめることになります。

ただレビュアーによっては探索的な後ろ向き研究でも検定の多重性を調整するようにコメントをする方がいます(悲しいかな…)。このような場合には「検証的研究ではないのでp値での判断では妥当ではなく、推定値に基づいて議論すべき!」とズバッと回答しましょう!
まとめ
今回は検定の多重性の問題について解説しました!
検定をくり返すことで研究全体のαエラーが事前に定めていた有意水準を超えてしまうので、統計学的にはNGです。ただ検証的な研究では、研究全体のαエラーを調整して、検定の多重性の問題を解決することができます。探索的研究の場合は検定の多重性を調整するのは難しい場合が多いので、オッズ比などの効果量をメインに報告しましょう!



コメント