医学研究では群間比較をするときに検定が用いられます。連続値の場合はt検定、カテゴリカルデータの場合はカイ二乗検定など、エンドポイントの型によって検定の種類は変わってきます。
ただエンドポイントの型以外にも検定には注意すべき点があります!
それはデータが相関しているとき。
データが相関しているときには、対応のある検定を行う必要があります!
ではどのような状況でデータが相関するのか?相関しているときにはどのような解析があるのか?について解説します!
この記事のpoint!
- 対応のあるデータとは相関のあるデータのこと
- 対応のある検定は対応のあるデータを比較するときに使われる
- 対応のあるデータのときに対応のある検定を行うと検出力が高くなる!
対応のある・対応のない検定とは?
比較するデータが相関しているかどうかの違い
対応のある・対応のない検定の違いは検定で比較されるデータが相関しているかどうかです!
対応のある検定は群間でデータが相関しているときに、対応のない検定は群間でデータが独立なときに使われます。
では相関するデータとはどのようなデータでしょうか。
相関するデータの例は以下になります!
相関しているデータの例
- 同一集団の治療前と治療後のデータ
- マッチング後のマッチングペアのデータ
対応のある検定も対応のない検定も比較しているものは同じ
ただ対応のある検定と対応のない検定で見ているもの、比較しているものは同じです。
例えば、平均値を比較する対応のあるt検定と対応のないt検定では、帰無仮説はどちらも「群間で平均値に差がない」になります。
変わっているのは検定統計、ひいてはp値の計算方法。
計算はソフトウェアが自動で行ってくれるので、適切に選択できることを第一に考えましょう!
対応のある検定は不要?
対応のあるデータのときは対応のある検定!
見ているものが同じなら「データが相関してるとか関係ないじゃん!」と思われるかもしれません。
ただ比較する群間データが相関する場合は対応のある検定を使うことをおすすめします!
というのも、相関するデータを比較するときには対応のない検定より対応のある検定の方が検出力が高くなります!
つまり、対応のある検定の方がp値が小さくなることになり、有意差が検出しやすくなります。
実際のデータで確認!
それでは実際に対応のあるデータを用いて、対応のある検定と対応のない検定を比較してみましょう!
「ある治療の効果を検証するために、治療前の平均と治療後の平均を比較したい」という状況を考えてみましょう。
本当の結果として治療前の平均が10、治療後の平均が10.5、相関係数を0.7としてデータを発生させてみます。
本当の結果は神のみぞ知る真実の値で、実際は知ることができない値です。
このとき、50人分のデータをとってくると以下のようになりました。正の相関なのでグラフは右肩上がりになります。
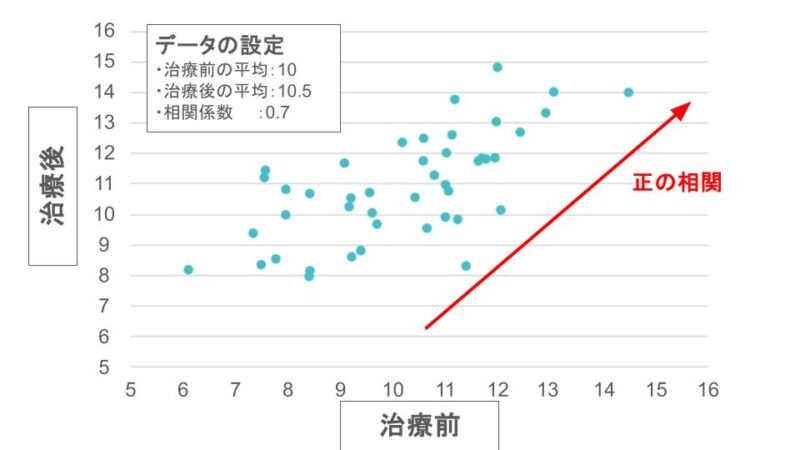
これらのデータは連続値なのでt検定を使って比較してみましょう!
対応のないt検定と対応のt検定は以下のようになりました。計算はRを使って行っています。
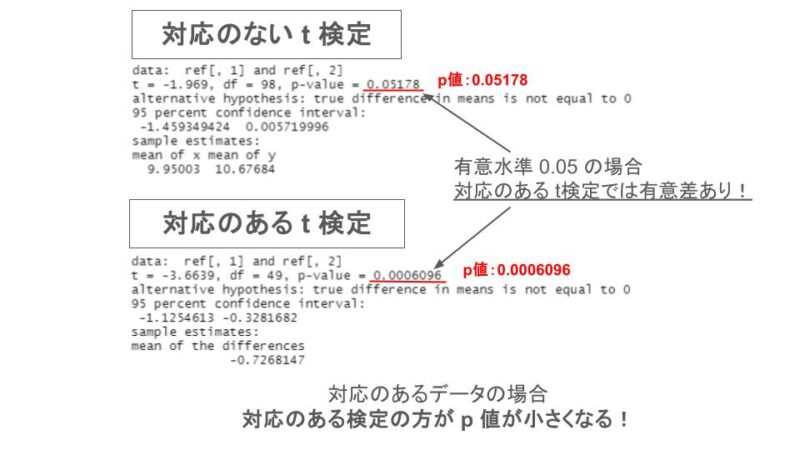
対応のないt検定のp値は0.05178、対応のあるt検定のp値は0.0006096になりました。よく使われる有意水準0.05であれば、対応のないt検定では有意差なし、対応のあるt検定では有意差あり、ということになります!
群間差の10.5-10=0.5に臨床的に意味があるのならば、対応のないt検定ではその差を見逃すことになりますね。
このように対応のあるデータでは対応のある検定を使った方がp値は小さくなります!
対応のある検定にはどんな検定がある?
比較したいものそれぞれに適した検定方法があります。
比較したいものに対応する対応のある検定は以下になります。

何を比較したいかによって適切に解析手法を選択しましょう!
まとめ
今回は対応のある検定とはなにかについて解説しました。
まとめ
- 対応のある検定:相関のあるデータを比較する方法
- 対応のない検定:独立なデータを比較する方法
対応のあるデータを解析する時は対応のある検定を使うことで検出力を上げることができます。
そのため、対応のあるデータには対応のある検定を使いましょう!




コメント