多変量解析は交絡因子を説明変数に加えて、治療効果をバイアスなく推定したり、予後因子や予測因子を探索するために使われます。
複数の交絡因子がある場合には多変量解析は有用な方法ですが、その変数選択には注意が必要です。
今回は多変量解析で注意が必要な多重共線性とその対応策について解説します!
多重共線性とその問題は?

多重共線性(multicollinearity)とは「相関する因子を同時に説明変数に加えると推定が不安定になる」という現象のことです。
多変量解析を行っていてオッズ比やハザード比の推定値が<0.0001や>999.99のように極端な値になったことはないでしょうか?
信頼区間が他の因子に比べて広くなってしまったことはないでしょうか?
このような場合には多重共線性が起こっていることが考えられます!
この原因は因子の組み合わせで作られる層のサンプルサイズが小さくなってしまうからです。
例えば、性別(男性/女性)と年齢(65歳未満/65歳以上)の例で見ていきましょう。
左の表では(男性, 65歳未満)、(男性, 65歳以上)、(女性, 65歳未満)、(女性, 65歳以上)の症例数はどれも25例になっていますが、一方、右の表では(男性, 65歳未満)、(女性, 65歳以上)に50例と偏っています。
このような場合、左の表の場合は多重共線性が起こらないですが、右の表の場合は(男性, 65歳以上)、(女性, 65歳未満)の症例数がいないため、これらの層での推定ができず推定が不安定になってしまいます。

多重共線性が起こった結果をそのまま報告してしまうと、間違った結果を報告してしまうことになるので注意しましょう!
多重共線性の確認方法

多重共線性が起こっているか確認する方法は2点あります。
多重共線性の確認方法
- (解析前)分割表や散布図を描いてみる
- (解析後)推定値が極端な値になっていないか確認する
それぞれの方法を見ていきましょう!
分割表や散布図を描いてみる
多重共線性は「説明変数が相関しているとき」に起こる現象でした。
そのため、多重共線性が起こらないように事前に因子間に相関がないかを確認する必要があります。
相関の確認の方法として分割表や散布図を描く方法があります。
分割表はカテゴリカルのデータの相関を、散布図は連続値のデータの相関を
確認するときに使われます。
それぞれ相関している場合には以下のような結果になります。
- 分割表:対角のセルにデータが集まっている
- 散布図:データが右肩上がり、右肩下がりに分布している
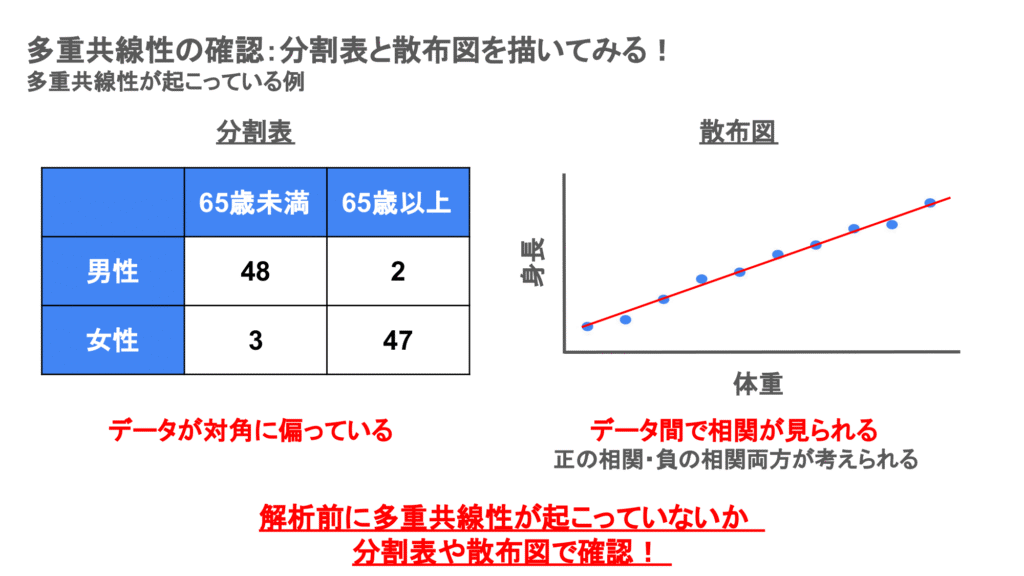
多重共線性を避けるために解析前に分割表や散布図を描いて因子の分布を確認するように心がけましょう!
推定値が極端な値になっていないか確認する
解析した後に多重共線性が起こっていないか確認するためには、
推定値が極端な値になっていないかを確認しましょう!
例えば、推定値が<0.01と0に近い値、や>999.99のようにあまりに大きな値になっていると
多重共線性が起こっていることが考えられます。
また場合によっては、推定値が臨床的に理解できる水準であっても、
信頼区間が広くなりすぎることがあります。
このような場合にも多重共線性が起こっていることが考えられます。
そのため、推定値やその信頼区間が他の因子と比べておかしな値になっていないか、を確認して多重共線性が起こっていないか確認しましょう!
多重共線性にはどのように対応する?

多重共線性が起こっている場合にはどのように解析していくべきでしょうか?
以下では多重共線性が起こっている場合の対応策について見ていきましょう!
相関する因子を説明変数から外す
一番シンプルな方法は相関する因子を説明変数から除外してしまうことです。
つまり、2つの因子が相関している場合には、どちらか一方のみ説明変数に加えて、一方は説明変数からは除外します。そうすることで多重共線性が起こる因子は除外されるので推定が安定します。
では相関している因子のどれを残し、どれを除外すればよいでしょうか?
個人的には、交絡因子として強い方を残すことを勧めたいと思います。
つまり、既報にて交絡因子として報告されている方を残す、ということです。
ただ交絡因子としての強さが分からないこともあると思います。
そのような場合には、それぞれの因子を加えたまたは除いた解析を複数行いましょう。
例えば、因子1と因子2が相関しているときには、
「因子1を入れて因子2を除いた解析」と「因子2を入れて因子1を除いた解析」
の2種類の解析を行います。
この結果があまり変わらなければ、結果の頑健性を示すことにもつながります。
そのため、多重共線性が起こっている場合には、相関する因子を説明変数から除外して解析を行いましょう!
多重共線性を無視する(!?)
2つ目の対策は多重共線性を無視するという方法です。
「それでは多重共線性が残ったままだよ!」と思われたかもしれません。
その通り!多重共線性は残ったままです(!?)
ただ「2つの治療効果を比較したい」という研究で、
治療効果に関わらないところで多重共線性が起こっている場合はどうでしょうか?
例えば、治療Aと治療Bを比較したいときに、相関している因子1と因子2を説明変数に加えた場合、治療Aと治療Bの推定値は安定しており、因子1と因子2の推定が不安定になることがあります。
このように興味がある治療Aと治療Bの推定に問題がない場合、因子1と因子2の推定には興味がないため、多重共線性を無視して因子1と因子2は説明変数として残しておく、という考え方もあります。
そのため、何に興味があるか、何に興味がないか、と優先度をつけて、
場合によっては多重共線性を無視する、という選択肢もあります。
まとめ

今回は多重共線性の問題とその対応方法について解説しました!
多重共線性が起こることで推定が不安定になってしまうので、
多重共線性が起こらないように解析前にデータの相関を確認したり、
解析後に推定値が極端な値になっていないか確認したりする必要があります。
もし多重共線性が起こっている場合には、
相関している因子を除いたり、
推定の必要がある因子かを判断したりして、
多重共線性が起こっていない結果を報告するようにしましょう!




コメント