2つの因子の関係性を評価する指標として相関係数が使われます。
相関係数は因子の関係性を定量的に評価できるため、理解が得られやすい概念ですが、一方で誤用されている例も少なくありません。
この記事では相関係数の正しい解釈と代表的な相関係数の計算方法について解説します!
相関=「連続的な2つの変数の直線的な関係」

相関係数で評価される相関とは何でしょうか?
相関(correlation)とは「連続的な2つの変数の直線的な関係」のことです。
相関の定義で最も重要なのが、相関は「直線的な関係」ということ。
つまり、直線的ではない関連は相関とは呼びません!
そのため、直線的な関係がない場合は「相関がある(correlated)」ではなく、「関係がある(assosiated)」と記載する方がよいでしょう。
例えば、以下のような場合には、「相関」ではなく「関係がある」ということになります。
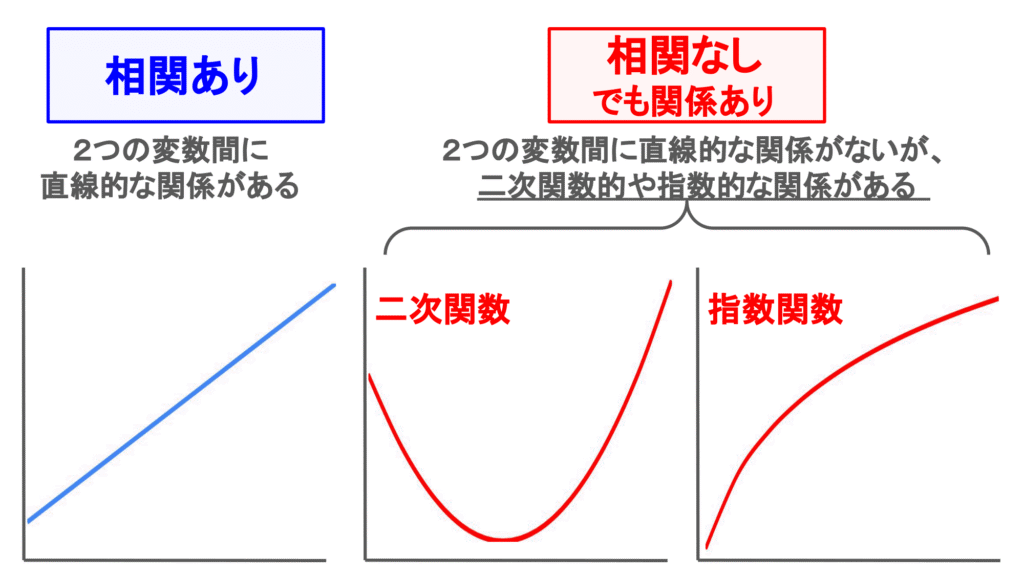
また相関があることは「因果関係がある」とは異なることにも注意が必要です。つまり、相関がある2つの変量がある場合、どちらかが原因で、どちらかが結果である、ということは分からないので論文のdiscussionの記載には注意しましょう!
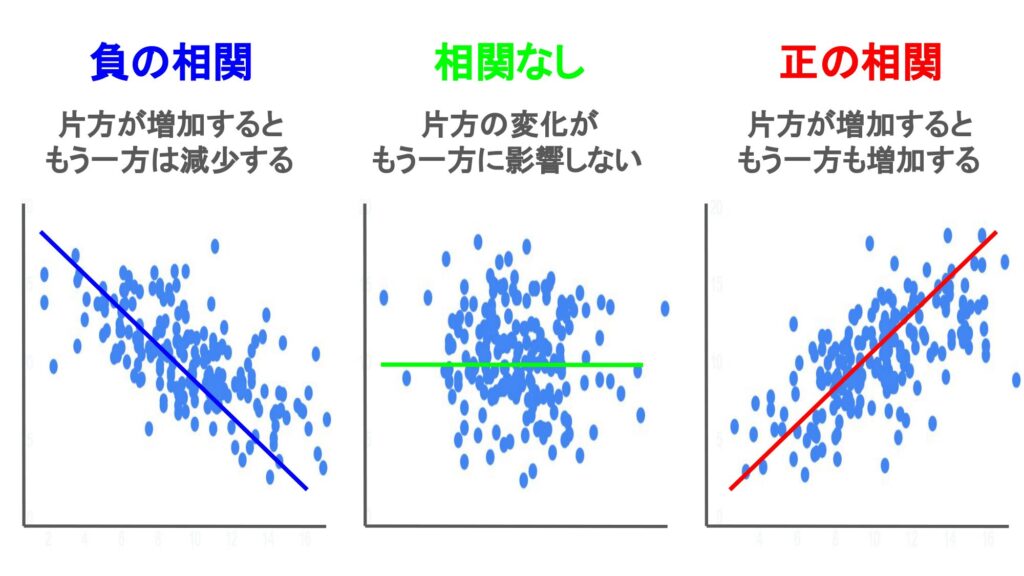
相関係数とは「連続的な2つの変数の直線的な関係の強さ」を示す指標

相関係数の見方
相関係数(correlation coefficient)は「連続的な2つの変数の直線的な関係の強さ」を示す指標です。
相関係数は一般に$\rho$(ロー)で表現され、-1~1の範囲をとります($-1\le\rho\le1$)。
相関係数は正、負の場合で「相関の方向」が変わり、絶対値の大きさが大きくなるほど相関の強さが強くなります。
| $-1\le\rho<0$ | 負の相関(片方が上がればもう一方は下がる) |
| $\rho=0$ | 相関なし |
| $0<\rho\le1$ | 正の相関(片方が上がればもう一方は下がる) |
相関の強さの目安
では相関係数がどの程度であれば、「相関が強い」と言えるでしょうか?
相関係数の強さの目安にはよく以下のようなGuilfordの基準が使われます。
| $|\rho|=0$ | 相関なし |
| $0<|\rho|<0.2$ | 非常に弱い相関 |
| $0.2\le|\rho|<0.4$ | 弱い相関 |
| $0.4\le|\rho|<0.6$ | そこそこ強い相関 |
| $0.6\le|\rho|<0.8$ | 強い相関 |
| $0.8\le|\rho|<1.0$ | 非常に強い相関 |
| $|\rho|=1$ | 完全な相関 |
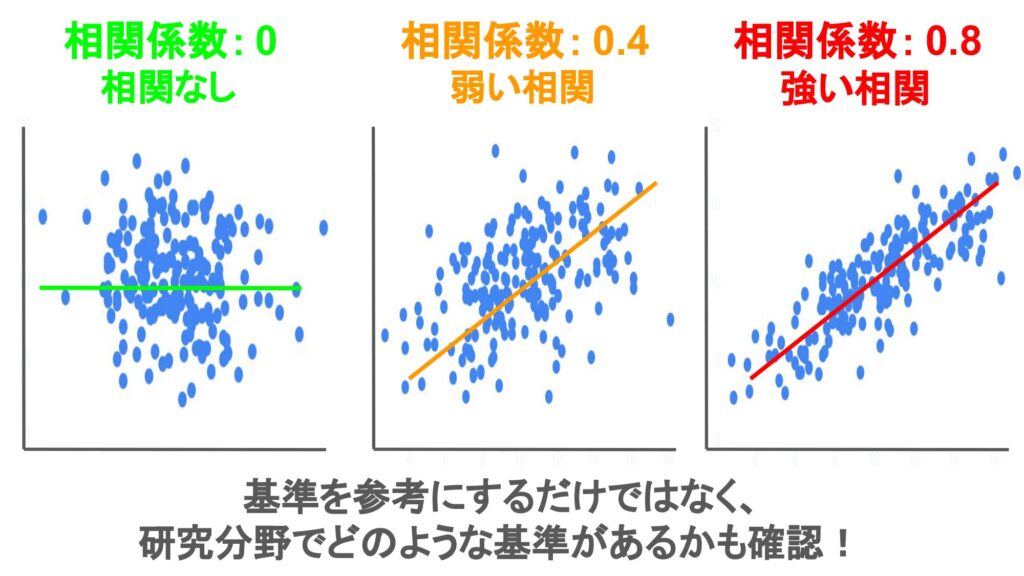
ただし、この基準はどんな研究領域で当てはまる基準というわけではないため、研究領域の過去の研究からどのような基準で判断されているか、確認した上で相関の強さを議論する必要があります!
代表的な相関係数 – Pearsonの相関係数・Spearmanの順位相関係数

では、相関係数はどのように計算すればよいでしょうか?
今回は以下の代表的な2種類の方法を解説します!
代表的な相関係数
- Pearsonの相関係数
- Spearmanの順位相関係数
Pearsonの相関係数
Pearsonの相関係数は「2つの変数の直線的な関係」を評価する相関係数です。
Pearsonの相関係数を計算する上で必要となる前提が、「2つの変数が連続的に正規分布に従うこと」です。つまり、相関を調べたい2つの変数がそれぞれ左右対称にばらついていることが必要になります。
Pearsonの相関係数は各変数の標準偏差と2つの変数の共分散を使って計算します。標準偏差は各変数のばらつきを、共分散は2つの変数の関係の強さを示す指標です。Pearsonの相関係数は2つの変数の共分散を各変数の標準偏差の積で割ることで算出されます。
Pearsonの相関係数の計算方法
$\rho = \frac{変数1と変数2の共分散}{変数1の標準偏差\times変数2の標準偏差}$
実際に以下の10例の体重と身長のデータから相関係数を計算してみましょう!
体重は平均65kgを中心に標準偏差10で正規分布に従ってばらついており、身長は平均170cmを中心に標準偏差5で正規分布に従ってばらついています。
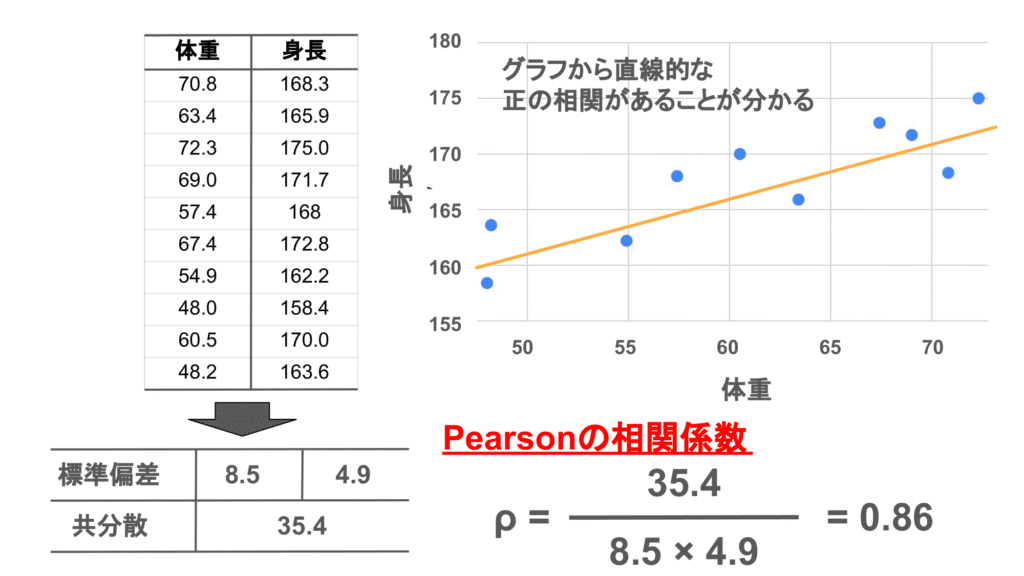
このデータでは体重と身長の標準偏差はそれぞれ8.5、4.9となり、共分散は35.4となりました。このとき、Pearsonの相関係数は$35.4/(8.5\times4.9)=0.86$と計算されます。
先ほどのGuilfordの基準では「非常に強い相関」ということになりますね!
Spearmanの順位相関係数
Spearmanの相関係数はデータを順序データに変換してPearsonの相関係数の式で計算した相関係数です。
このようにデータを変形することで、データが正規分布に従っていない場合でも相関係数を計算することができます!
Spearmanの相関係数を計算する上で注意してほしいことが「Spearmanの相関係数は直線的な関係=相関を示していない」ということです。
そのため、Spearmanの相関係数がー1に近い場合には一方が増加すればもう一方が増加する、1に近い場合には一方が増加すればもう一方は減少する、ということのみを示します。
実際にSpearmanの相関係数を計算してみましょう!
データはPearsonの相関係数を計算したときと同じデータを用います。
Spearmanの相関係数を計算するときにはまずデータをそれぞれ順位データに変換します。
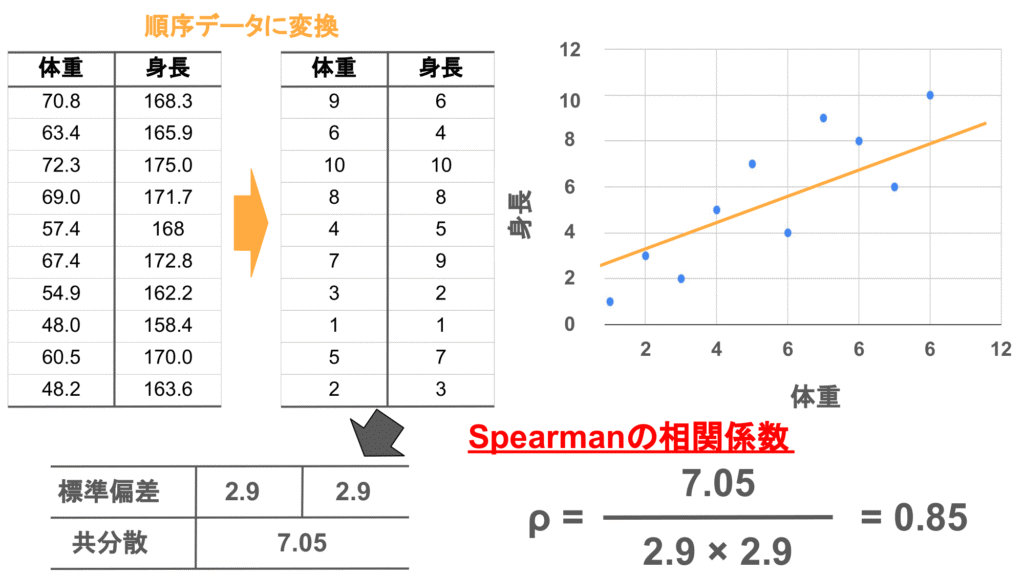
変換した順位データでは体重と身長の標準偏差はそれぞれ2.9、2.9となり、共分散は7.05となりました。このとき、Spearmanの相関係数は$7.05/(2.9\times2.9)=0.85$と計算されます。
こちらも先ほどのGuilfordの基準では「非常に強い相関」ということになりますね!
Pearsonの相関係数とSpearmanの相関係数のどちらを使うべき?

ここまでPearsonの相関係数とSpearmanの相関係数について説明しました。
ではPearsonの相関係数とSpearmanの相関係数、どちらを使うべきでしょうか?
Pearsonの相関係数とSpearmanの相関係数を使い分ける上で重要なポイントは以下の3点です!
Pearsonの相関係数とSpearmanの相関係数を使い分けるポイント
- データは正規分布に従っているか
- 2変量に直線的な関係があるか
- 外れ値はないか
データが正規分布に従っているか
Pearsonの相関係数は「データが正規分布に従っているか」という分布を前提としたパラメトリックな相関係数でした。一方、Spearmanの相関係数はそのような前提を必要とせず、データが正規分布に従っていなくとも使うことができるノンパラメトリックな相関係数です。
そのため、データが正規分布に従っていない場合にはPearsonの相関係数、正規分布に従っていない場合にはSpearmanの相関係数の相関係数を使うのがよいでしょう!
2変量に直線的な関係があるか
Pearsonの相関係数は「2変量に直線的な関係があるか」が分かるのに対して、Spearmanの相関係数で分かるのは「2変量に関係があるか」ということのみです。
そのため、散布図を描いてみて、2変量に直線的な関係がある場合にはPearsonの相関係数、2変量に直線的な関係がある場合にはSpearmanの相関係数の相関係数を使うのがよいでしょう!
外れ値はないか
Pearsonの相関係数は相関係数をそのまま数値を使って相関係数を計算していたのに対して、Spearmanの相関係数はデータを順位データに変換して相関係数を計算しています。
そのため、Pearsonの相関係数は外れ値があると、外れ値に値が引っ張られてしまい、相関係数に影響を受けてしまいます。それに対して、Spearmanの相関係数は順位データとしてデータを処理するため、外れ値の影響が小さくなります。
実際に以下のように外れ値が一つある場合の相関係数を計算してみましょう!
データは先ほどの体重と身長のデータに外れ値を1例追加しています。
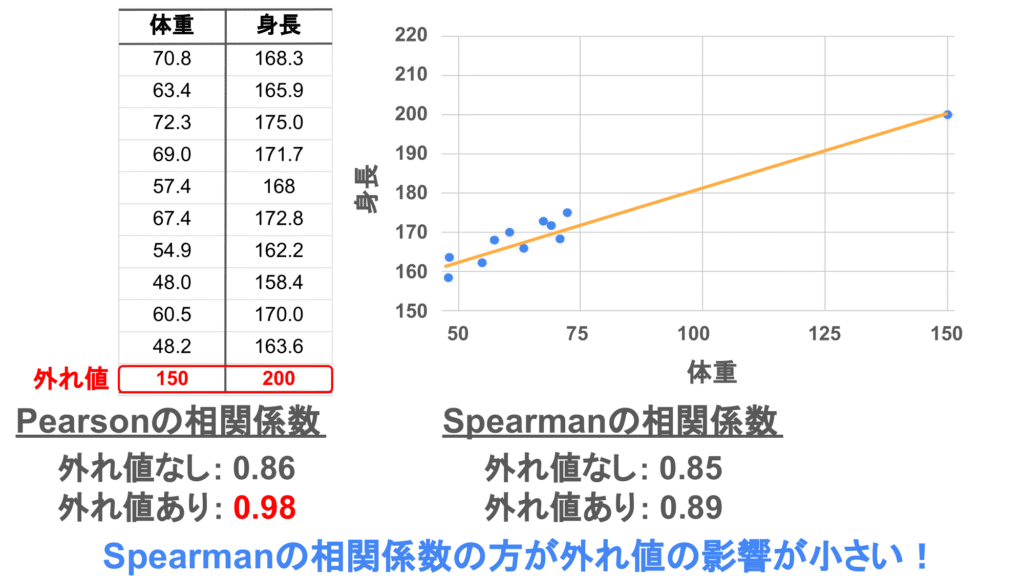
Pearsonの相関係数とSpearmanの相関係数をそれぞれ計算すると、Pearsonの相関係数は0.98、Spearmanの相関係数は0.89になります。外れ値がないときの相関係数が約0.85だったため、Pearsonの相関係数は外れ値の影響を受ける一方で、Spearmanの相関係数は外れ値の影響が受けにくいことが分かります。
そのため、外れ値がある場合はSpearmanの相関係数を使う方がよいでしょう!
まとめ

今回は相関係数の解釈と相関係数の計算方法を解説しました!
相関係数にはPearsonの相関係数とSpearmanの相関係数がよく使われますが、それぞれ特徴があるので理解していただけたならうれしいです!





コメント