医学研究には2つの検査法が一致しているかを評価することを目的とした研究があります。
一致率を評価するためには相関係数がよく使われます。ただ相関係数は線形関係を評価している指標であり、一致していないときに何故一致していないか、は議論することはできません。
そこで使われるのがBland-Altmanプロットというグラフを使った方法です!
Bland-Altmanプロットはデータの差を散布図としてプロットすることにより、一致率の評価を行います。
この記事ではBland-Altmanプロットの解釈とExcelでの作成方法を解説します!
Bland-Altmanプロットとは?

Bland-Altmanプロットは2つのデータ一致率を評価するグラフのことです。
Bland-Altmanは日本語ではブランド-アルトマンと読みます。
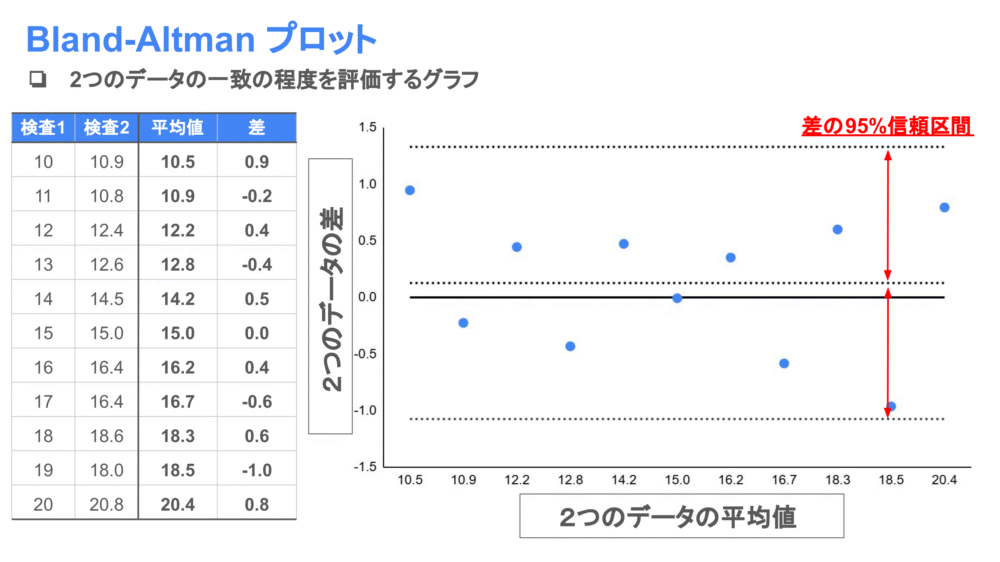
Bland-AltmanプロットはX軸に対応する2つのデータの平均値、Y軸に対応する2つのデータの差をプロットして作成します。
また場合によっては、差の平均値とその95%信頼区間をグラフに描くことがあります。
例えば以下のプロットでは、
データが差0を中心にばらついており、差の95%信頼区間内に収まっているので、
データの一致率は高いと考えられます。
Bland-Altmanプロットのチェックポイント

実際にいくつかのBland-Altmanプロットの例を見て、それぞれ解釈を考えていきましょう!
Bland-Altmanプロットでチェックしてほしいのは以下のポイントです。
- バイアスが含まれていないか
- 2つのデータに関数的な関係がないか
一致率の高いデータの場合
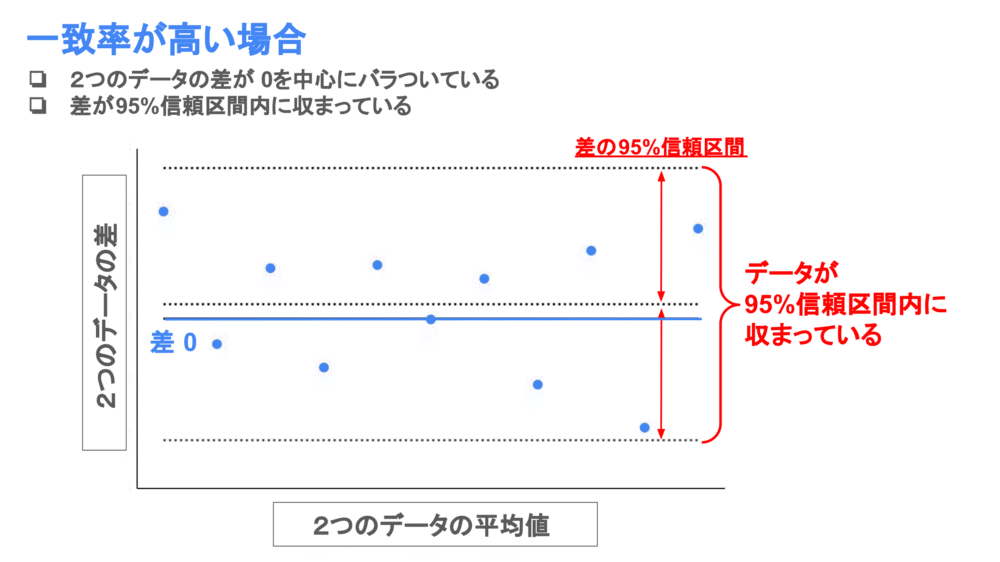
まずは標準的な一致率の高いデータの場合です。
一致率が高いときにはデータが差0を中心にばらついており、差の95%信頼区間内に収まっています。
バイアスがないかを確認
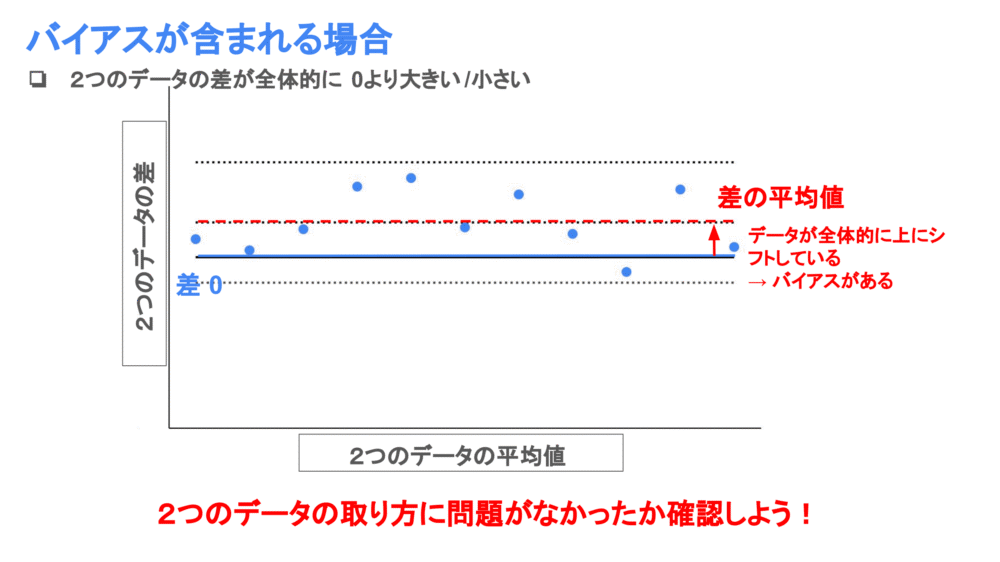
データが95%信頼区間に収まっていても注意が必要なときがあります。
それはデータが上か下一方向にズレている場合。
例えば上の図ではデータが全体的に上にズレています。つまり、片方の検査は大きな値がでやすいという特徴があります。
このように2つのデータの差が全体的に0より大きい/小さい場合には、バイアスがあると判断できます。
そのため、このようなBland-Altmanプロットでは一致率が高いとはいえません。
こんなときには、データの取り方に問題がある可能性があるため、一度データを見直してみましょう!
比例関係など特別な関係がないか確認
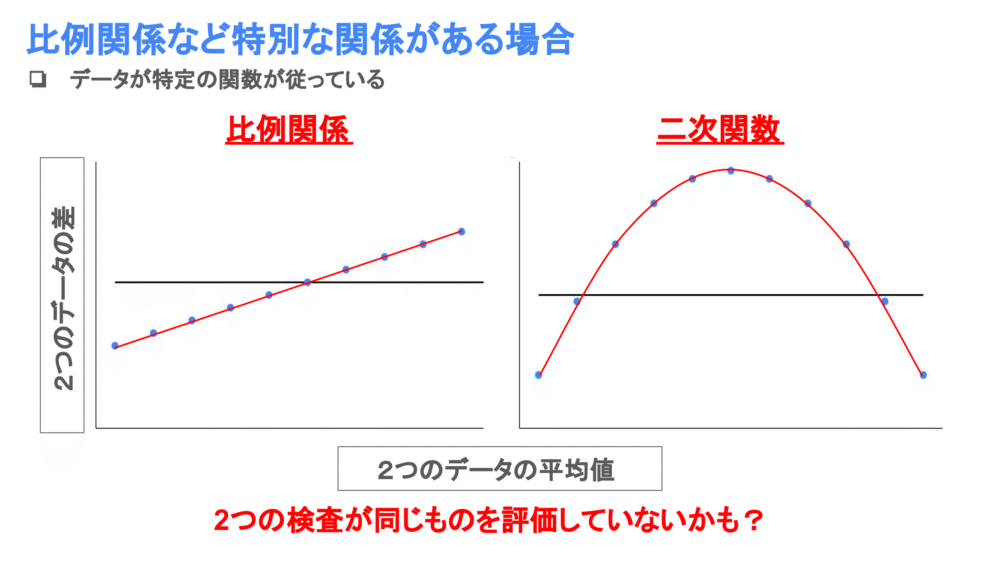
Bland-Altmanプロットではデータが何かの関数に従っていないかも確認しましょう!
例えば左図では比例関係、右図では二次関数のような関係があります。
このような場合、2つのデータの一致率が高いとは言えません。
またそもそも検査が同じものを評価していない可能性があるので、検査法を見直してみましょう!
ExcelでBland-Altmanプロットを描いてみよう!

実際にBland-Altmanプロットを描いてみましょう!
Bland-Altmanプロットを描く手順は以下の通りです。
Bland-Altmanプロットを描く手順
- 2つのデータの平均値と差を計算する
- 散布図でX軸に平均値、Y軸に差をプロットする
- 差の95%信頼区間を計算する
それぞれ順番に見ていきましょう!
使用するデータ
使用するデータは以下の11個の仮想データです。
どのデータも差は±1.0に収まっているので数値上は差がないと考えられそうです。
(相関係数やグラフで確認することも重要ですが、このように数値で一度確認しておくことも重要です!)
| 検査1 | 検査2 |
|---|---|
| 10 | 10.9 |
| 11 | 10.8 |
| 12 | 12.4 |
| 13 | 12.6 |
| 14 | 14.5 |
| 15 | 15.0 |
| 16 | 16.4 |
| 17 | 16.4 |
| 18 | 18.6 |
| 19 | 18.0 |
| 20 | 20.8 |
対応するデータの平均値と差を計算
Bland-Altmanプロットを描くには初めに各データの組の平均値と差を計算します。
平均値はAVERAGE関数、差は引き算(-)を使って計算できます。
以下の場合、行ごとに以下のように関数を入力して計算します。
- 平均値:“=AVERAGE(A2:B2)”
- 差:“B2-A2”
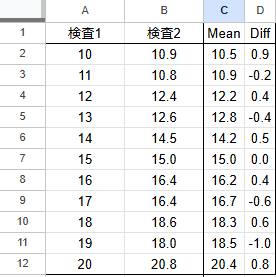
それぞれ平均値と差を計算すると以下の通りになります。
| 検査1 | 検査2 | 平均値 | 差 |
|---|---|---|---|
| 10 | 10.9 | 10.5 | 0.9 |
| 11 | 10.8 | 10.9 | -0.2 |
| 12 | 12.4 | 12.2 | 0.4 |
| 13 | 12.6 | 12.8 | -0.4 |
| 14 | 14.5 | 14.2 | 0.5 |
| 15 | 15.0 | 15.0 | 0.0 |
| 16 | 16.4 | 16.2 | 0.4 |
| 17 | 16.4 | 16.7 | -0.6 |
| 18 | 18.6 | 18.3 | 0.6 |
| 19 | 18.0 | 18.5 | -1.0 |
| 20 | 20.8 | 20.4 | 0.8 |
2つのデータの平均値と差をプロットする
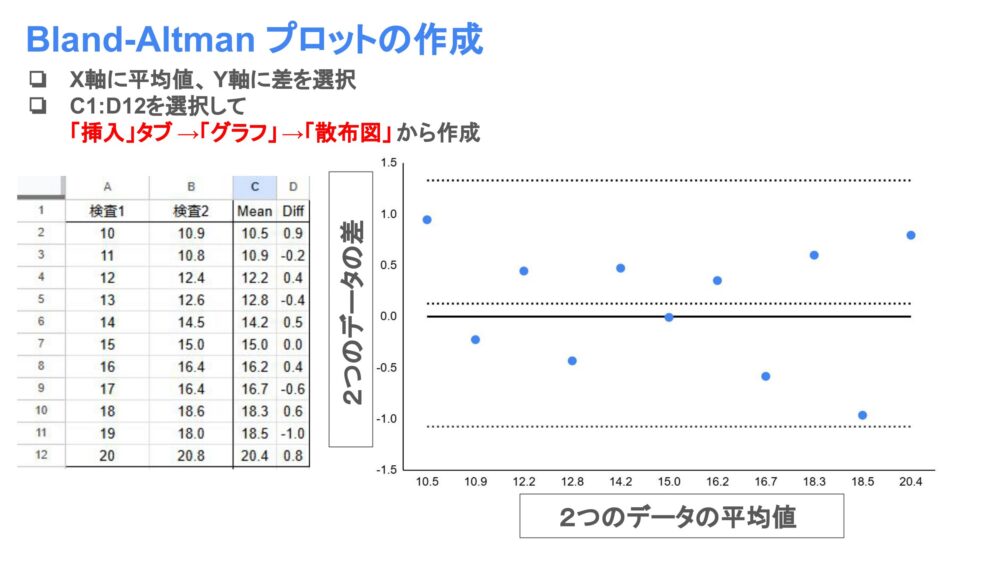
最後にX軸にデータの平均値、Y軸にデータの差をプロットしましょう。
これでBland-Altman plotは完成です!
上の「Bland-Altmanプロットのチェックポイント」で解説した誤差や特別な関係がないか確認してみましょう!
今回は系統的な誤差はなく、比例関係などもありませんので、
データは一致していると見て問題なさそうです。
95%信頼区間も計算してみよう!
データが誤差内に収まっているかを明示するために95%信頼区間も計算してみましょう!
差の95%信頼区間は以下の式で計算します。
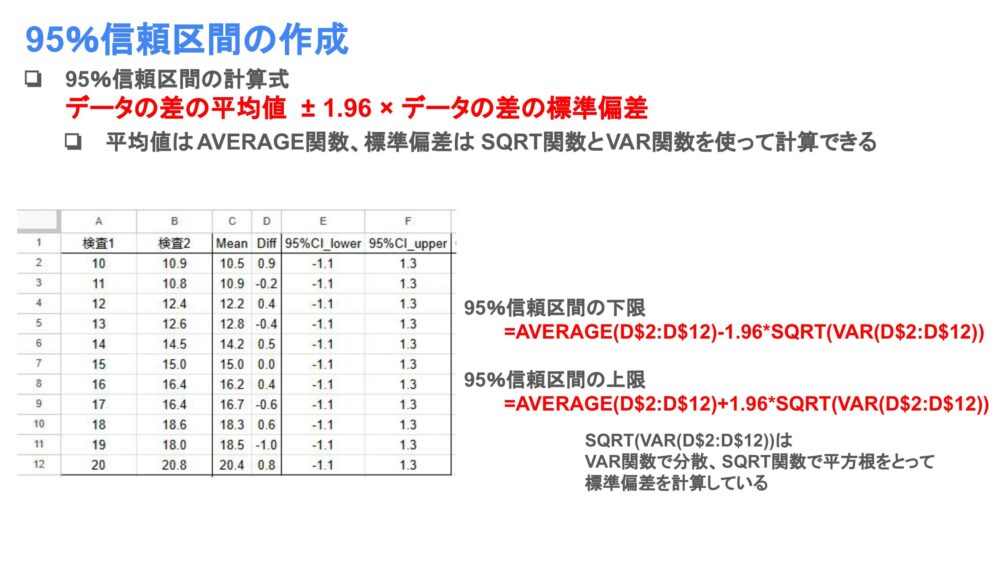
差の95%信頼区間の計算式
データの差の平均値±1.96×データの差の標準偏差
データの差の標準偏差はSQRT関数とVAR関数を使って以下のように計算することができます。
95%信頼区間の下限は-1.1、上限は1.3と計算でき、差はこの範囲に収まっているので、このデータの一致率は高いと言えるでしょう。
まとめ

今回はBland-Altman plotの見方とExcelでの描き方を解説しました!
Bland-Altman plotはX軸に2つのデータの平均値、Y軸に2つのデータの差をプロットして、
2つのデータが一致しているかを評価するグラフです。
もしデータが0を中心にばらついており、95%信頼区間内であれば、2つのデータは一致していると判断できます。
最後にExcelでのBland-Altman plotの描き方も解説しましたので、参考にしてみてください!




コメント